Conservation of Angular Momentum is a fundamental principle in physics that states that the total angular momentum of a system remains constant if no external torques act on it. Angular momentum is a vector quantity that describes the rotational motion of an object or a system of objects.
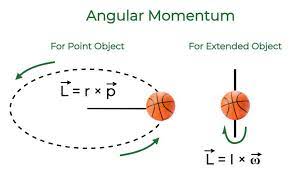
The angular momentum of an object is defined as the product of its moment of inertia (a measure of an object’s resistance to rotational motion) and its angular velocity (the rate at which it rotates around an axis). Mathematically, angular momentum (L) is expressed as L = Iω, where I is the moment of inertia and ω is the angular velocity.
According to the conservation of angular momentum, if the net external torque acting on a system is zero, the total angular momentum of the system remains constant over time. This means that the sum of the angular momenta of all the individual objects within the system remains unchanged.
In another terms, when an object or a system undergoes a change in its moment of inertia, its angular velocity will change in such a way that the total angular momentum is conserved.
This principle has various applications and implications in different areas of physics:
- Celestial Mechanics: It is crucial in understanding the motion of celestial bodies, such as planets and satellites, in their orbits. As a planet moves closer to or farther from the Sun, its moment of inertia changes, leading to a corresponding change in its angular velocity, ensuring conservation of angular momentum.
- Rotational Motion: When a spinning object, such as a spinning top or a gyroscope, experiences a change in its moment of inertia (e.g., due to the redistribution of mass), its angular velocity adjusts to maintain the conservation of angular momentum.
- Atomic Physics: It is fundamental in atomic physics, particularly in understanding electron orbitals and transitions between energy levels. The theory plays a role in determining the allowed angular momentum states of electrons within atoms.
- Sports and Athletics: The principle of conservation of angular momentum is evident in activities such as figure skating, diving, and gymnastics. Athletes can alter their body positions to change their moment of inertia, thereby adjusting their angular velocity and achieving complex manoeuvres while conserving angular momentum.
The conservation of angular momentum is a powerful concept that provides insights into the behavior of rotating systems and has broad implications in various areas of physics and everyday life.

Important Links