To calculate the inverse of a 3×3 matrix, you can follow these steps:
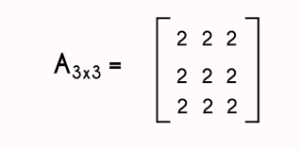
Consider the matrix you want to invert. Let’s denote it as matrix A:
- A = | a11 a12 a13 | | a21 a22 a23 | | a31 a32 a33 |
- Calculate the determinant of matrix A. Denote it as det(A). You can use the following formula:det(A) = a11(a22a33 – a32a23) – a12(a21a33 – a31a23) + a13(a21a32 – a31a22)
- Check if the determinant (det(A)) is equal to zero. If det(A) is zero, the matrix A does not have an inverse.
- If the determinant is non-zero, proceed to find the adjugate of matrix A. The adjugate, denoted as adj(A), is the transpose of the cofactor matrix of A. The cofactor of each element in matrix A is calculated by multiplying the determinant of the 2×2 matrix obtained by removing the element’s row and column by a factor of (-1) raised to the power of the sum of its row and column indices.
For example, the cofactor of a11 is given by: C11 = (-1)^(1+1) * det(A11) C12 = (-1)^(1+2) * det(A12) C13 = (-1)^(1+3) * det(A13) Where A11, A12, A13 represent the 2×2 submatrices obtained by removing the first row and first column, first row and second column, and first row and third column, respectively. The adjugate matrix is obtained by transposing the cofactor matrix:
adj(A) = | C11 C21 C31 | | C12 C22 C32 | | C13 C23 C33 |
Finally,
Calculate the inverse of matrix A by dividing the adjugate matrix by the determinant: A^(-1) = (1 / det(A)) * adj(A)
Let’s go through an example to illustrate the process:
Suppose we have the following matrix A:
A = | 1 2 3 | | 0 4 5 | | 1 0 6 |
Calculate the determinant of A:
det(A) = 1(46 – 05) – 2(06 – 15) + 3(00 – 14) = 1(24) – 2(-5) + 3(0) = 24 + 10 + 0 = 34
Since the determinant (34) is non-zero, we proceed to find the adjugate of A. Calculate the cofactors of each element in A:
C11 = (-1)^(1+1) * det(A11) = 1(4) – 5(0) = 4 C12 = (-1)^(1+2) * det(A12) = -(0(6) – 1(5)) = -5 C13 = (-1)^(1+3) * det(A13) = 1(0) – 4(0) = 0 C21 = (-1)^(2+1) * det(A21) = -(2(6) – 3(5)) = 3 C22 = (-1)^(2+2) * det(A22) = 1(6) – 3(1) = 3 C23 = (-1)^(2+3) * det(A23) = -(1(6) – 3(0)) = -3 C31 = (-1)^(3+1) * det(A31) = 2(5) – 4(4) = -6 C32 = (-1)^(3+2) * det(A32) = -(1(5) – 4(1)) = -1 C33 = (-1)^(3+3) * det(A33) = 1(4) – 2(1) = 2
Transpose the cofactor matrix to obtain the adjugate:
adj(A) = | C11 C21 C31 | | C12 C22 C32 | | C13 C23 C33 | = | 4 3 -6 | | -5 3 -1 | | 0 -3 2 |
Calculate the inverse of A by dividing the adjugate matrix by the determinant:
A^(-1) = (1 / det(A)) * adj(A) = (1 / 34) * | 4 3 -6 | | -5 3 -1 | | 0 -3 2 |
Therefore, the inverse of matrix A is:
A^(-1) = | 4/34 3/34 -6/34 | | -5/34 3/34 -1/34 | | 0/34 -3/34 2/34 |