Kepler law of planetary motion are some of the most important contributions to the field of astronomy. They explain the movement of planets around the sun and have helped scientists understand the solar system. In this article, we will delve into the three laws of planetary motion and understand the concept of the same.
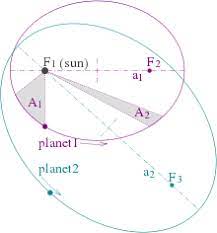
Table of Contents
Kepler’s First Law
The first law of Kepler, also known as the law of ellipses, explains the orbit of a planet around the sun. It states that the path of each planet around the sun is an ellipse with the sun at one of the two foci. The eccentricity of the ellipse determines the shape of the orbit. An eccentricity of 0 indicates a circular orbit, while an eccentricity greater than 0 indicates an elliptical orbit. The law of ellipses provides an accurate explanation of the observed orbits of the planets in our solar system.
Kepler’s Second Law
The second law of Kepler, also known as the law of equal areas, explains the speed at which a planet moves around the sun. It states that the line that connects a planet to the sun sweeps out equal areas in equal times. This means that a planet moves faster when it is closer to the sun and slower when it is farther away. This law provides an explanation for the observed phenomenon that planets move faster when they are closer to the sun and slower when they are farther away.
Kepler’s Third Law
The third law of Kepler, also known as the law of harmonies, explains the relationship between the orbital period and distance of a planet from the sun. It states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit. The semi-major axis is half the distance across the longest part of the ellipse. The law of harmonies provides an accurate way to calculate the period and distance of a planet from the sun.
Applications of Kepler Law of Planetary Motion
Kepler’s laws have several practical applications. They are used to determine the orbits of planets, asteroids, and comets. They are also used in the design of spacecraft trajectories for missions to other planets. Kepler’s laws are also used to study the motion of stars in binary star systems and to search for exoplanets in other star systems.
Limitations of Kepler Law of Planetary Motion
While Kepler’s laws provide an accurate explanation of the motion of planets in our solar system, they have some limitations. They assume that the planets move in a vacuum without any external forces acting on them. In reality, planets are affected by the gravitational pull of other planets and objects in the solar system. Kepler’s laws also do not take into account the effects of relativity, which become significant at high speeds and in strong gravitational fields.
Conclusion
Kepler’s laws of planetary motion are a fundamental concept in astronomy. They provide a precise explanation of the movement of planets around the sun and have numerous practical applications. However, they have some limitations and do not account for external forces acting on planets or the effects of relativity. Despite these limitations, Kepler’s laws remain a cornerstone of modern astronomy and continue to be studied and applied today.
Summary
- Kepler’s laws explain the motion of planets around the sun.
- The first law states that a planet’s orbit is an ellipse with the sun at one focus.
- The second law states that a planet moves faster when it is closer to the sun.
- The third law states that a planet’s orbital period is related to its distance from the sun.
- Kepler’s laws have practical applications in determining orbits and designing spacecraft trajectories.
- They are also used to study binary star systems and search for exoplanets.
- However, they have limitations and do not account for external forces or the effects of relativity.
- Kepler’s laws remain a cornerstone of modern astronomy.
- They are a fundamental concept in understanding the solar system.
- Kepler’s laws continue to be studied and applied in astronomy today.
Important Links