Resistance of Conductor is a fundamental property of conductive materials that plays a vital role in electrical engineering and various applications. Understanding the concept of resistance is crucial for designing efficient electrical systems, ensuring safety, and optimizing performance.
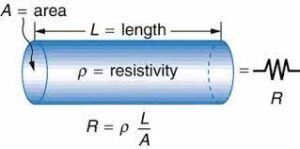
Table of Contents
What is Resistance of a Conductor?
Resistance, denoted by the symbol “R,” is a measure of the opposition encountered by an electric current as it flows through a conductor. It quantifies the difficulty of electron flow and is responsible for converting electrical energy into heat. The unit of resistance is the ohm (Ω), named after the German physicist Georg Simon Ohm.
Resistance Calculator
Factors Affecting Resistance
Material: Each material exhibits a specific resistance property. Materials with high resistivity, such as rubber or glass, impede the flow of electrons more than materials with low resistivity, like copper or silver. Copper, due to its excellent conductivity, is commonly used in electrical wiring.
Length: Resistance is directly proportional to the length of a conductor. Longer conductors have higher resistance because the electric current has to travel a greater distance, encountering more opposition.
Cross-Sectional Area: Resistance is inversely proportional to the cross-sectional area of a conductor. A larger area allows more space for electron flow, resulting in lower resistance.
Temperature: Temperature influences resistance. In most conductors, resistance increases with an increase in temperature due to the greater vibration of atoms, impeding the movement of electrons. However, some materials, such as semiconductors, exhibit different temperature-resistance characteristics.
How to calculate the Resistance of a conductor?
To calculate the resistance of a conductor, you can use Ohm’s Law or the formula for resistance, which takes into account the material’s resistivity, length, and cross-sectional area. Here’s how you can calculate resistance:
- Determine the resistivity (ρ) of the conductor material: The resistivity is a material property and can be obtained from reference tables or online resources. It is typically measured in ohm-meters (Ω·m).
- Measure the length (L) of the conductor: Determine the length of the conductor for which you want to calculate the resistance. Ensure that the length is measured in meters (m) to maintain consistency.
- Measure the cross-sectional area (A) of the conductor: Determine the cross-sectional area of the conductor perpendicular to the current flow. The area should be measured in square meters (m²).
- Calculate the resistance (R) using the formula: The formula for resistance is R = (ρ * L) / A, where R is the resistance in ohms (Ω), ρ is the resistivity in ohm-meters (Ω·m), L is the length of the conductor in meters (m), and A is the cross-sectional area of the conductor in square meters (m²).
Example: Let’s say you have a copper wire with a length of 10 meters, a cross-sectional area of 2 square millimeters (2 x 10^-6 square meters), and the resistivity of copper is 1.7 x 10^-8 ohm-meters.
Plugging the values into the formula, we get: R = (1.7 x 10^-8 Ω·m * 10 m) / (2 x 10^-6 m²) = 8.5 x 10^-3 ΩTherefore, the resistance of the copper wire is 8.5 milliohms (mΩ).
Note: Ensure that all units are consistent when performing the calculation. If the units of length or area are different, convert them to the appropriate unit (e.g., meters for length, square meters for area) before calculating the resistance.
Understanding the concept of resistance is essential in electrical engineering. From designing electrical circuits to optimizing energy efficiency, resistance plays a vital role. By considering the factors affecting resistance and applying Ohm’s Law, engineers can calculate and manage resistance effectively. Mastering the principles of resistance enables the development of safe and efficient electrical systems that power our modern world.
Read More