Simple Harmonic Motion I UPSC Notes

Simple Harmonic Motion (SHM) is a type of periodic motion that occurs when a restoring force proportional to the displacement from the equilibrium position acts on an object. In other words, it is a special form of oscillatory or vibratory motion that repeats itself over time.

Key Characteristics of Simple Harmonic Motion

1. Periodic Motion: It repeats itself at regular intervals of time.
2. Restoring Force: The restoring force is directly proportional to the displacement from the equilibrium position. It acts in the opposite direction to the displacement, trying to bring the object back towards the equilibrium position.
3. Equilibrium Position: The position at which the object experiences no net force and is at rest is called the equilibrium position. In the absence of external forces, the object would stay at this position.
4. Frequency and Period: The frequency (f) is the number of oscillations per unit time, measured in Hertz (Hz), and the period (T) is the time it takes for one complete oscillation.
   They are inversely related: f = 1/T.
5. Amplitude: The maximum displacement of the object from the equilibrium position is called the amplitude.
6. Examples of Simple Harmonic Motion:
   • A mass-spring system: A mass attached to a spring exhibits simple harmonic motion when displaced from its equilibrium position.
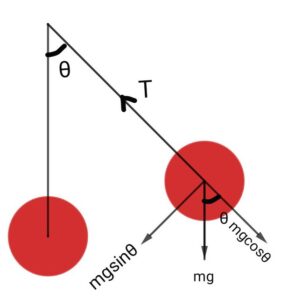
   • A pendulum: A simple pendulum, when displaced and released, undergoes such situation

The mathematical representation of this motion can be expressed using trigonometric functions. For an object in simple harmonic motion with displacement $x$ from the equilibrium position, the equation is often given by:

$x(t)=A\cdot \cos (\omega t+\varphi )$

Where:

• $A$ is the amplitude (maximum displacement),
• $\omega$ is the angular frequency ($\omega =2\pi f$),
• $t$ is time,
• $\varphi$ is the phase constant.

Simple Harmonic Motion is a fundamental concept in physics and applies to various natural phenomena, including sound waves, light waves, and mechanical vibrations. It provides a mathematical framework for understanding and describing periodic motion in diverse physical systems.

Read: UPSC Physical Optional Syllabus