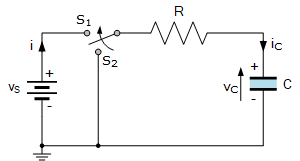
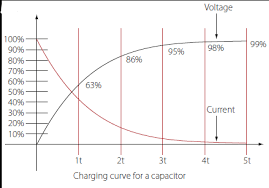
Time constant is a amount of time that a system takes to reach a new equilibrium or to change its state significantly. In the context of physics, the time constant is often associated with systems that exhibit exponential decay or growth. It represents the time required for a quantity, such as voltage, current, temperature, or charge, to reach approximately 63.2% (1 – 1/e) of its final value in response to a step input or disturbance.
Table of Contents
RC Time Constant Calculator
Time Constant (τ) =
Definition
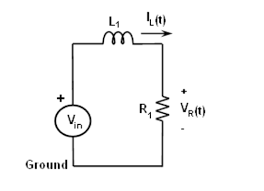
It is determined by the product of the resistance (R) and the capacitance (C) or the product of the resistance (R) and the inductance (L) of the circuit, depending on the type of circuit element involved. For an RC circuit (resistor-capacitor), the time constant (τ) is equal to R multiplied by C, while for an RL circuit (resistor-inductor), it is equal to L divided by R.
It is often denoted by the Greek letter tau (τ). A larger time constant indicates a slower response, while a smaller one implies a faster response. It is an important parameter for analyzing the transient behavior of systems and determining the speed of response or the settling time of a system.
The concept can be applied to various other systems and processes beyond electrical circuits, including mechanical systems, chemical reactions, biological systems, and more. In each case, the it provides insight into the characteristic response time of the system.
What is Time Constant Formula
The formula depends on the type of circuit or system involved. Here are the formulas for the time constant in commonly encountered circuits:
Time Constant of RC circuit
RC Circuit (Resistor-Capacitor): τ = R * C where R is the resistance in ohms and C is the capacitance in farads.
Time Constant of RL circuit
RL Circuit (Resistor-Inductor): τ = L / R where L is the inductance in henries and R is the resistance in ohms.
It’s important to note that these formulas assume ideal circuit elements and do not take into account factors such as parasitic capacitance, inductance, or resistance, which can affect the actual response time of a circuit.
Additionally, the concept of time constant can be applied beyond circuits, such as in exponential decay or growth processes, where the formula may differ based on the specific situation.
Question
Question: A capacitor of capacitance 10 μF is connected in series with a resistor of resistance 100 kΩ. If an initial charge of 20 μC is stored on the capacitor, determine the time constant of the circuit and calculate the charge on the capacitor after 1 second.
Solution: The time constant (τ) of an RC circuit is given by the formula:
τ = R * C
where R is the resistance and C is the capacitance.
Given: C = 10 μF (microfarads) R = 100 kΩ (kiloohms)
To find the time constant (τ):
τ = R * C = (100 × 10^3 Ω) * (10 × 10^(-6) F) = 1 second
The time constant of the circuit is 1 second.
To calculate the charge on the capacitor after 1 second:
Q(t) = Q(0) * e^(-t/τ)
where Q(t) is the charge on the capacitor at time t, Q(0) is the initial charge on the capacitor, t is the time, and τ is the time constant.
Given: Q(0) = 20 μC (microcoulombs) t = 1 second τ = 1 second
Q(1) = Q(0) * e^(-1/1) = 20 μC * e^(-1) ≈ 20 μC * 0.3679 ≈ 7.358 μC
The charge on the capacitor after 1 second is approximately 7.358 μC.
Question: In an RL circuit, an inductor with an inductance of 0.5 H is connected in series with a resistor of 10 Ω. If the current through the circuit is initially 2 A and the time constant of the circuit is 0.2 seconds, determine the current through the circuit after 1 second.
Solution: τ of an RL circuit is given by the formula:
τ = L / R
where L is the inductance and R is the resistance.
Given: L = 0.5 H (henries) R = 10 Ω (ohms) τ = 0.2 seconds
To find the current through the circuit after 1 second:
I(t) = I(0) * e^(-t/τ)
where I(t) is the current through the circuit at time t, I(0) is the initial current, t is the time, and τ is the time constant.
Given: I(0) = 2 A (amperes) t = 1 second τ = 0.2 seconds
I(1) = I(0) * e^(-1/0.2) = 2 A * e^(-5) ≈ 2 A * 0.0067 ≈ 0.0134 A
The current through the circuit after 1 second is approximately 0.0134 A or 13.4 mA.
Important Links