Decimal to Octal Conversion Examples

Decimal to octal conversion is the process of converting a number from the decimal number system (base 10) to the octal number system (base 8). The octal number system uses eight digits: 0, 1, 2, 3, 4, 5, 6, and 7.

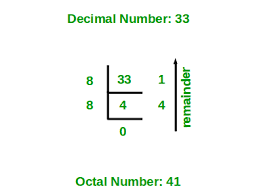
To convert a decimal number to octal, you can follow these steps:

1. Start with the decimal number you want to convert.
2. Divide the decimal number by 8.
3. Write down the remainder obtained from the division as the rightmost digit in the octal representation.
4. Divide the quotient obtained from the previous step by 8 again.
5. Write down the remainder as the next digit to the left in the octal representation.
6. Repeat steps 4 and 5 until the quotient becomes zero.
7. The resulting digits, read from left to right, form the octal representation of the decimal number.

Here’s an example to illustrate the process:

Let’s convert the decimal number 189 to octal.

Step 1: Divide 189 by 8: 189 ÷ 8 = 23 remainder 5

Step 2: Divide the quotient (23) by 8: 23 ÷ 8 = 2 remainder 7

Step 3: Divide the quotient (2) by 8: 2 ÷ 8 = 0 remainder 2

Since the quotient has become zero, we stop dividing.

Step 4: The remainders obtained in reverse order are 2, 7, and 5.

Therefore, the octal representation of the decimal number 189 is 275.

So, the decimal number 189 is equivalent to 275 in octal.