Octal to Decimal Converter

Octal to decimal conversion is the process of converting a number from the octal number system (base 8) to the decimal number system (base 10). The decimal number system uses ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Get the Octal to Decimal Converter at the bottom of the post.

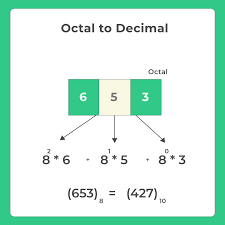
To convert an octal number to decimal, you can follow these steps:

1. Start with the octal number you want to convert.
2. Identify the place value of each digit in the octal number, starting from the rightmost digit. The rightmost digit has a place value of 8^0 (which is 1), the next digit to the left has a place value of 8^1 (which is 8), the next digit has a place value of 8^2 (which is 64), and so on.
3. Multiply each digit of the octal number by its corresponding place value.
4. Add up the results of the multiplication from step 3 to get the decimal equivalent of the octal number.

Here’s an example to illustrate the process:

Let’s convert the octal number 753 to decimal.

Step 1: Write down the octal number 753.

Step 2: Identify the place value of each digit:

• The rightmost digit (3) has a place value of 8^0 = 1.
• The next digit (5) has a place value of 8^1 = 8.
• The leftmost digit (7) has a place value of 8^2 = 64.

Step 3: Multiply each digit by its place value: 3 * 1 = 3 5 * 8 = 40 7 * 64 = 448

Step 4: Add up the results: 3 + 40 + 448 = 491

Therefore, the octal number 753 is equivalent to the decimal number 491.

So, the decimal equivalent of the octal number 753 is 491.