Capacitor and Capacitance - Licchavi Lyceum

What is a Capacitor?

A capacitor is a passive electrical component that stores electrical energy in an electric field. It consists of two conductive plates separated by an insulating material called the dielectric. When a voltage is applied across the plates, an electric field develops across the dielectric, causing positive charge to accumulate on one plate and negative charge on the other. Capacitors are widely used in electronic circuits for various purposes, like filtering, energy storage, and signal processing.

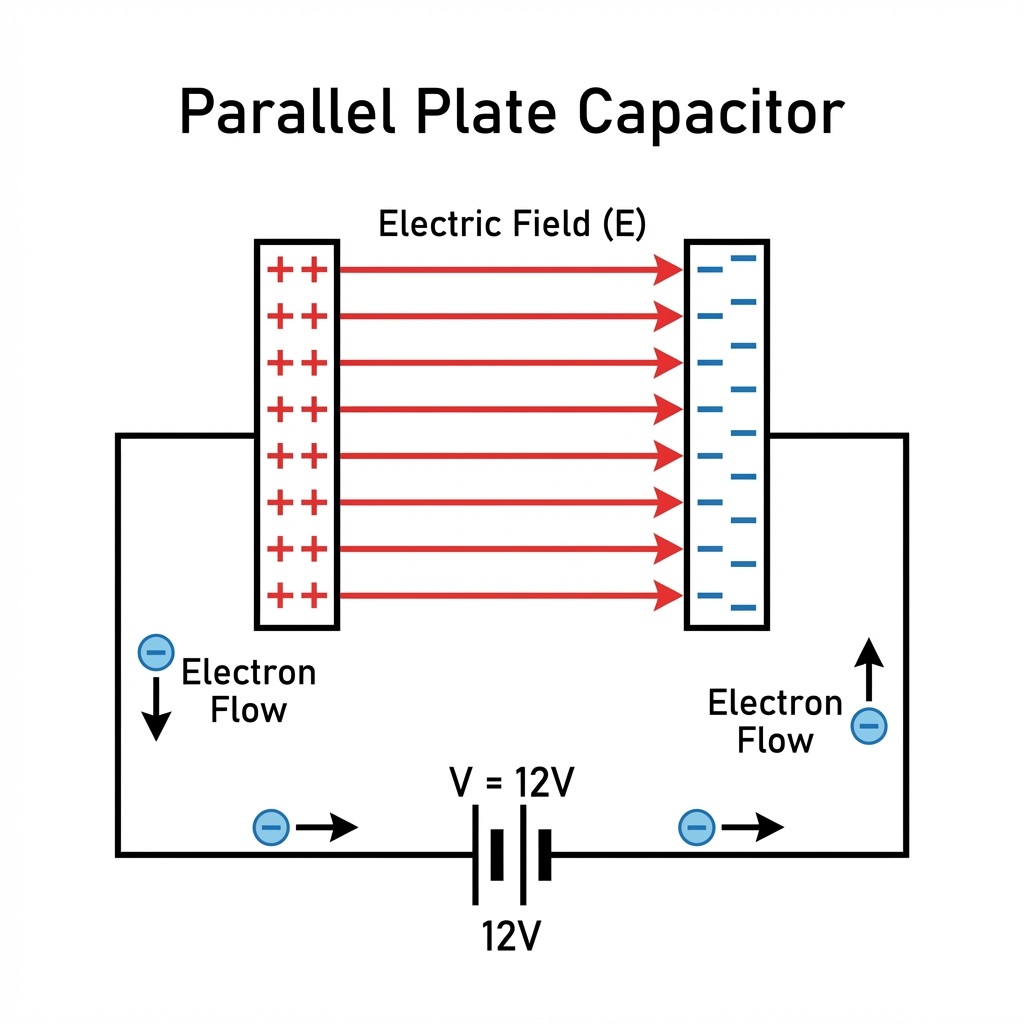
Components of a Capacitor

Conductive Plates: Typically made of metal.
Dielectric: An insulating material that separates the plates and can be made of materials such as air, glass, ceramic, or plastic.

Question on Capacitor

Q. What happens when a voltage is applied across the plates of a capacitor?

A. It generates a magnetic field
B. It develops an electric field across the dielectric
C. It causes current to flow continuously
D. It creates a mechanical vibration

Correct Answer:
B. It develops an electric field across the dielectric

Explanation:
When a voltage is applied across the plates of a capacitor, an electric field develops across the dielectric material between the plates. This electric field is responsible for the storage of electrical energy in the capacitor.

Q. What is the role of the dielectric material in a capacitor?

A. To conduct electricity between the plates
B. To create resistance to current flow
C. To separate the conductive plates and store energy in the electric field
D. To increase the current flow between the plates

Correct Answer:
C. To separate the conductive plates and store energy in the electric field

Explanation:
The dielectric material in a capacitor serves to separate the two conductive plates and allows the capacitor to store energy in the form of an electric field. The dielectric also increases the capacitor’s ability to store charge by reducing the potential for charge leakage between the plates.

Q. Which of the following is NOT a common use of capacitors in electronic circuits?

A. Energy storage
B. Signal processing
C. Data storage
D. Filtering

Correct Answer:
C. Data storage

Explanation:
Capacitors are widely used for energy storage, signal processing, and filtering in electronic circuits. However, data storage is not a common use for capacitors. Data storage is typically handled by other components such as memory chips or hard drives.

Capacitance

Capacitance is a measure of a capacitor’s ability to store charge per unit of voltage. It is denoted by the symbol $ C $ and is measured in farads (F). The capacitance value depends on the physical characteristics of the capacitor: the area of the plates ($ A $), the distance between the plates ($ d $), and the dielectric constant ($ \kappa $) of the insulating material.

The formula for capacitance is given by:

$ C = \kappa \epsilon_0 \frac{A}{d} $

Where:

$ C $ is the capacitance in farads.
$ \kappa $ is the dielectric constant of the material between the plates.
$ \epsilon_0 $ is the permittivity of free space ($ \approx 8.854 \times 10^{-12} \, \text{F/m} $).
$ A $ is the area of one of the plates in square meters.
$ d $ is the distance between the plates in meters.

Capacitance Formula

A capacitor is an electrical component that stores energy in the form of an electric field. The relationship between the charge ($ Q $), voltage ($ V $), and capacitance ($ C $) of a capacitor is fundamental to understanding its behavior in circuits.

The relationship between charge, voltage, and capacitance is given by the formula:

\[
Q = C \cdot V
\]

Where:

$ Q $ is the charge stored in the capacitor (in coulombs, $ \text{C} $).
$ C $ is the capacitance of the capacitor (in farads, $ \text{F} $).
$ V $ is the voltage across the capacitor (in volts, $ \text{V} $).

Consider a capacitor with a capacitance of $ 5 \, \mu\text{F} $ (microfarads) and a voltage of $ 12 \, \text{V} $ applied across it. The charge stored in the capacitor can be calculated as follows:

\[
Q = C \cdot V = 5 \times 10^{-6} \, \text{F} \times 12 \, \text{V} = 60 \times 10^{-6} \, \text{C} = 60 \, \mu\text{C}
\]

Characteristics of Capacitors

Energy Storage: Capacitors store energy in the electric field created between their plates.
Charge and Discharge: Capacitors can quickly charge and discharge, making them useful for applications requiring rapid energy transfer.
Voltage Rating: Every capacitor has a maximum voltage rating, beyond which the dielectric material may break down.

Applications of Capacitors

Filtering: In power supplies, capacitors smooth out voltage fluctuations.
Timing: In oscillators and timers, capacitors help determine the timing intervals.
Coupling and Decoupling: In signal processing, capacitors block DC components while allowing AC signals to pass.
Energy Storage: In applications like camera flashes and defibrillators, capacitors store and release large amounts of energy quickly.

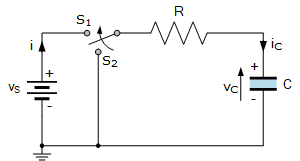
Time Constant of Series RC Circuit

The time constant of a series RC (resistor-capacitor) circuit, often denoted as
$ \tau $ (tau), is a measure of the time it takes for the voltage across the capacitor
to charge or discharge to approximately 63.2% of its final value. It is a key parameter
that characterizes the response of the RC circuit to a step input, such as the sudden
application or removal of a voltage source.

The time constant $ \tau $ is given by the product of the resistance $ R $ and the
capacitance $ C $ of the circuit:

\[ \tau = R \cdot C \]

Charging Process

When a voltage $ V $ is suddenly applied to an uncharged capacitor in series with a resistor,
the capacitor begins to charge. The voltage across the capacitor $ V_C(t) $ as a function of
time $ t $ during the charging process is given by:

\[ V_C(t) = V \left(1 – e^{-\frac{t}{RC}}\right) \]

After a time equal to $ \tau $, the voltage across the capacitor reaches about 63.2% of the applied voltage $ V $.

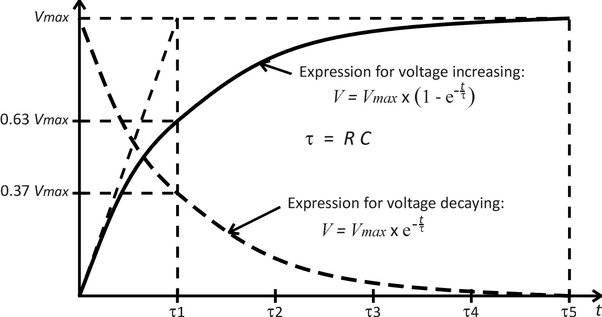
Discharging Process

If the capacitor is initially charged to a voltage $ V_0 $ and then allowed to discharge
through the resistor, the voltage across the capacitor $ V_C(t) $ during the discharging
process is given by:

\[ V_C(t) = V_0 \cdot e^{-\frac{t}{RC}} \]

After a time equal to $ \tau $, the voltage across the capacitor drops to about 36.8% of its initial value $ V_0 $.

Physical Interpretation

The time constant $ \tau $ represents the speed at which the capacitor charges or discharges.
A larger $ \tau $ means a slower charging or discharging process, while a smaller $ \tau $
means a faster process.

In practical terms, after a time period of about $ 5\tau $, the capacitor is considered to be fully charged or discharged, as the voltage will have reached over 99% of its final value.

Understanding the time constant is crucial in various applications, such as in the design of filters, timing circuits, and in the analysis of transient responses in electrical circuits.

Q1. What does the time constant ($ \tau $) represent in relation to a capacitor’s behavior?

A. The maximum voltage the capacitor can hold
B. The resistance offered by the capacitor
C. The speed at which the capacitor charges or discharges
D. The energy stored in the capacitor

Answer: C. The speed at which the capacitor charges or discharges

Explanation: The time constant ($ \tau $) represents the speed at which the capacitor charges or discharges. A larger $ \tau $ indicates a slower process, while a smaller $ \tau $ indicates a faster process.

Q2. After approximately how many time constants ($ \tau $) is a capacitor considered to be fully charged or discharged?

A. $ \tau $
B. $ 2\tau $
C. $ 5\tau $
D. $ 10\tau $

Answer: C. $ 5\tau $

Explanation: In practical terms, after a time period of about $ 5\tau $, the capacitor is considered to be fully charged or discharged, as the voltage will have reached over 99% of its final value.

Q3. Why is understanding the time constant important in the design of filters and timing circuits?

A. It helps to determine the physical size of the capacitor
B. It indicates the maximum current the capacitor can handle
C. It is crucial for the design of filters, timing circuits, and analysis of transient responses
D. It measures the thermal stability of the capacitor

Answer: C. It is crucial for the design of filters, timing circuits, and analysis of transient responses

Explanation: Understanding the time constant is crucial in various applications, such as in the design of filters, timing circuits, and in the analysis of transient responses in electrical circuits.

Q4. Find the Time Constant of the RC circuit given below.

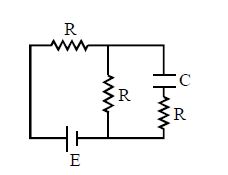
Solution:

Step 1: Apply Thevenin’s Theorem

Convert the circuit into a Thevenin’s Equivalent Circuit by performing the following steps:

Open circuit the terminals of the capacitor $ C $.
Short circuit the voltage source.

Now, the circuit becomes a combination of series and parallel resistors. Specifically, resistors $ R $ are in parallel with $ R $, and the resultant is in series with another $ R $. Hence, the equivalent resistance $ R_{\text{eq}} $ becomes:

\[
R_{\text{eq}} = \frac{3R}{2}
\]

Step 2: Draw the Equivalent Thevenin Circuit

The voltage source in the Thevenin equivalent circuit becomes $ \frac{E}{2} $, and the resistance becomes $ \frac{3R}{2} $. This series configuration is connected with the capacitor $ C $.

Step 3: Calculate Time Constant

The time constant $ \tau $ of the circuit is given by the product of the equivalent resistance and the capacitance:

\[
\tau = \left(\frac{3R}{2}\right) \cdot C = \frac{3RC}{2}
\]

Equivalent Capacitance

Capacitors in Series

When capacitors are connected in series, the equivalent capacitance ($C_{\text{eq}}$) is given by:

\[
\frac{1}{C_{\text{eq}}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \cdots + \frac{1}{C_n}
\]

Example Calculation:

For three capacitors in series with capacitances $C_1 = 2 \, \mu\text{F}$, $C_2 = 3 \, \mu\text{F}$, and $C_3 = 6 \, \mu\text{F}$:

\[
\frac{1}{C_{\text{eq}}} = \frac{1}{2} + \frac{1}{3} + \frac{1}{6}
\]

\[
\frac{1}{C_{\text{eq}}} = 0.5 + 0.333 + 0.167 = 1.0
\]

\[
C_{\text{eq}} = \frac{1}{1.0} = 1 \, \mu\text{F}
\]

Comment: The equivalent capacitance for capacitors in series is always less than the smallest individual capacitor in the series. This configuration results in a lower overall capacitance because it is limited by the smallest capacitor’s ability to store charge.

Capacitors in Parallel

When capacitors are connected in parallel, the equivalent capacitance ($C_{\text{eq}}$) is given by:

\[
C_{\text{eq}} = C_1 + C_2 + C_3 + \cdots + C_n
\]

Example Calculation:

For three capacitors in parallel with capacitances $C_1 = 2 \, \mu\text{F}$, $C_2 = 3 \, \mu\text{F}$, and $C_3 = 6 \, \mu\text{F}$:

\[
C_{\text{eq}} = 2 + 3 + 6 = 11 \, \mu\text{F}
\]

Comment: The equivalent capacitance for capacitors in parallel is always greater than the largest individual capacitor in the parallel network. This configuration results in a higher overall capacitance, allowing more charge to be stored at the same voltage.

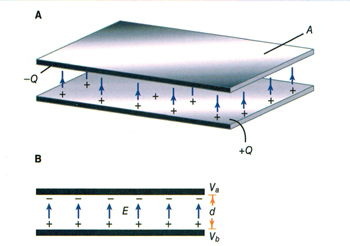
Electric Field Created by a Charged Capacitor

A capacitor consists of two conductive plates separated by an insulating material (dielectric). When a voltage is applied across the capacitor, an electric field is created between the plates due to the separation of charges. This electric field is central to the capacitor’s ability to store energy.

Electric Field ($ \mathbf{E} $)

The electric field ($ \mathbf{E} $) between the plates of a parallel plate capacitor is uniform and can be calculated using the following formula:

\[
\mathbf{E} = \frac{V}{d}
\]

Where:

$ \mathbf{E} $ is the electric field strength (in volts per meter, V/m).
$ V $ is the voltage across the capacitor (in volts, V).
$ d $ is the separation distance between the plates (in meters, m).

Charge Distribution

When a capacitor is charged, positive charge accumulates on one plate and negative charge on the other. This separation of charges creates the electric field. The magnitude of the charge ($ Q $) on each plate is related to the capacitance ($ C $) and the voltage ($ V $) by:

\[
Q = C \cdot V
\]

Electric Field Calculation

Given a capacitor with capacitance $ C $, plate area $ A $, and plate separation $ d $, the electric field can also be expressed in terms of the surface charge density ($ \sigma $):

\[
\sigma = \frac{Q}{A}
\]

Then the electric field ($ \mathbf{E} $) is:

\[
\mathbf{E} = \frac{\sigma}{\epsilon_0} = \frac{Q}{\epsilon_0 A}
\]

Where $ \epsilon_0 $ is the permittivity of free space ($ \epsilon_0 \approx 8.85 \times 10^{-12} \, \text{F/m} $).

Energy Stored in the Electric Field

The energy ($ U $) stored in the electric field of a capacitor is given by:

\[
U = \frac{1}{2} C V^2
\]

This energy is stored in the form of an electric field between the plates.

Example Calculation

Consider a parallel plate capacitor with the following parameters:

Capacitance: $ C = 10 \, \mu\text{F} $
Voltage: $ V = 5 \, \text{V} $
Plate separation: $ d = 0.01 \, \text{m} $
Plate area: $ A = 0.1 \, \text{m}^2 $

Calculate the electric field:

\[
\mathbf{E} = \frac{V}{d} = \frac{5 \, \text{V}}{0.01 \, \text{m}} = 500 \, \text{V/m}
\]

Calculate the surface charge density:

\[
Q = C \cdot V = 10 \times 10^{-6} \, \text{F} \times 5 \, \text{V} = 50 \times 10^{-6} \, \text{C} = 50 \, \mu\text{C}
\]

\[
\sigma = \frac{Q}{A} = \frac{50 \times 10^{-6} \, \text{C}}{0.1 \, \text{m}^2} = 500 \times 10^{-6} \, \text{C/m}^2 = 500 \, \mu\text{C/m}^2
\]

Calculate the electric field using surface charge density:

\[
\mathbf{E} = \frac{\sigma}{\epsilon_0} = \frac{500 \times 10^{-6} \, \text{C/m}^2}{8.85 \times 10^{-12} \, \text{F/m}} \approx 56.5 \times 10^6 \, \text{V/m}
\]

(Note: The discrepancy between the electric fields calculated by the two methods is due to simplified assumptions in the second method.)

Relative Permittivity of Insulating Materials

The relative permittivity (or dielectric constant) of a material is a measure of how much it can increase the capacitance of a capacitor compared to a vacuum. It is denoted by $ \epsilon_r $. Different insulating materials have different relative permittivity values, which affect their use in capacitors and other electrical components.

Material	Relative Permittivity ($ \epsilon_r $)
Vacuum	1.0
Air	1.0006
Paper	3.0 – 4.0
Mica	5.0 – 7.0
Glass	4.0 – 10.0
Porcelain	6.0
Polystyrene	2.5 – 2.7
Polyethylene	2.25
Silicon Dioxide	3.9
Water	80

The relative permittivity of a material determines how much it can increase the capacitance of a capacitor. A higher $ \epsilon_r $ value means the material is more effective at storing electrical energy. For example, water has a very high relative permittivity of 80, making it very effective at storing charge, but it is not typically used in capacitors due to its conductivity and other properties.

Mica, with a relative permittivity of 5.0 to 7.0, is commonly used in capacitors due to its stability, low loss, and ability to withstand high voltages. Similarly, materials like glass and porcelain are also used in various applications due to their relatively high dielectric constants and insulating properties.

Q. Which of the following insulating materials has the highest relative permittivity?

A. Air
B. Mica
C. Glass
D. Barium Titanate

Answer: D. Barium Titanate ($\varepsilon_r \approx 1200$)

Explanation: The relative permittivity (also known as the dielectric constant) is a measure of how much a material can hold electric charge in an electric field. Among the given materials, Barium Titanate has the highest relative permittivity of approximately 1200, making it highly effective in storing electrical energy compared to air, mica, and glass.

Licchavi Lyceum

What is a Capacitor?

Components of a Capacitor

Capacitance

Capacitance Formula

Characteristics of Capacitors

Applications of Capacitors

Time Constant of Series RC Circuit

Charging Process

Discharging Process

Physical Interpretation

Equivalent Capacitance

Capacitors in Series

Capacitors in Parallel

Electric Field Created by a Charged Capacitor

Electric Field (\( \mathbf{E} \))

Charge Distribution

Electric Field Calculation

Energy Stored in the Electric Field

Example Calculation

Relative Permittivity of Insulating Materials