Table of Contents
Magnetic Field
A magnetic field is a region around a magnetic material or a moving electric charge within which the force of magnetism acts.
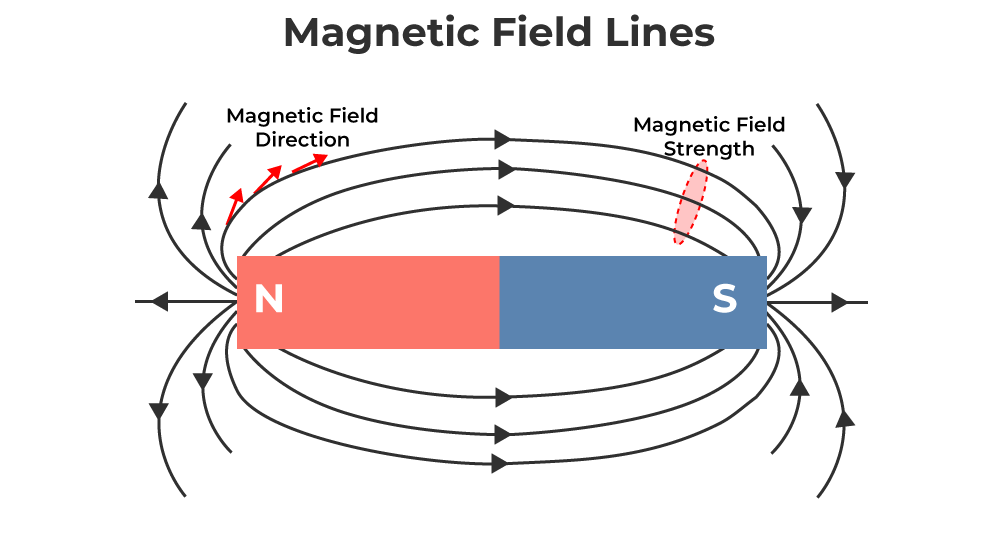
Magnetic Field Lines
Magnetic field lines are a visual representation of the magnetic field. They depict the direction and strength of the magnetic field.
- The direction of the magnetic field lines is from the north pole to the south pole of a magnet.
- The density of the field lines indicates the strength of the magnetic field; closer lines mean a stronger field.
Properties of Magnetic Field Lines
- Magnetic field lines never intersect.
- They form closed loops, starting from the north pole and ending at the south pole.
- Inside the magnet, the field lines run from the south pole back to the north pole, maintaining the closed-loop structure.
- Parallel Magnetic Lines of Force repel each other.
Sources of Magnetic Fields
- Permanent Magnets: Objects that produce their own persistent magnetic field.
- Electromagnets: Magnetic fields generated by electric currents. The field is proportional to the current and can be turned on or off.
- Earth’s Magnetic Field: The Earth itself acts as a giant magnet with a magnetic field extending from the magnetic north to the magnetic south pole.
Magnetic Force
A moving charge or a current-carrying conductor experiences a force when placed in a magnetic field.
The direction of the magnetic force is given by the right-hand rule: If the thumb of your right hand points in the direction of current and your fingers point in the direction of the magnetic field, your palm points in the direction of the force experienced by a positive charge.
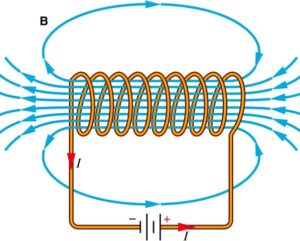
Magnetic Field Around a Current-Carrying Conductor
A straight conductor: The magnetic field forms concentric circles around the conductor, with the direction given by the right-hand thumb rule.
A solenoid: A coil of wire that generates a uniform magnetic field within its interior when an electric current passes through it.
Right-Hand Screw Rule
The right-hand screw rule is used to determine the direction of the magnetic field around a current-carrying conductor.
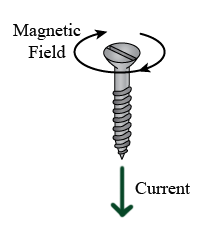
The right-hand screw rule is applied as follows:
- Hold a Screw in Your Right Hand: Imagine holding a right-handed screw in your right hand.
- Direction of Current: Point your thumb in the direction of the current
- Direction of Magnetic Field or Rotation: The direction in which your fingers curl, or the direction in which you would turn the screw to move it forward, indicates the direction of the magnetic field lines.
- Straight Conductor: For a straight conductor carrying an electric current, point your thumb in the direction of the current flow. Your curled fingers represent the direction of the magnetic field lines encircling the conductor.
- Solenoid: For a solenoid or a coil of wire carrying a current, curl your fingers in the direction of the current through the loops. Your thumb then points in the direction of the magnetic field inside the solenoid.
Mathematical Representation
Biot-Savart Law: Describes the magnetic field generated by an electric current.
\[
d\mathbf{B} = \frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{\hat{r}}}{r^2}
\]
- \( \mu_0 \): Permeability of free space
- \( I \): Current
- \( d\mathbf{l} \): A small segment of the current-carrying wire
- \( \mathbf{\hat{r}} \): Unit vector from the wire to the point of interest
- \( r \): Distance between the wire segment and the point
Ampère’s Law: Relates the integrated magnetic field around a closed loop to the electric current passing through the loop.
\[
\oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}}
\]
- \( \mathbf{B} \): Magnetic field
- \( d\mathbf{l} \): Differential length element of the closed loop
- \( I_{\text{enc}} \): Current enclosed by the loop
Magnetic Flux
Magnetic flux (\( \Phi \)) is the measure of the total magnetic field passing through a given area.
\[
\Phi = \mathbf{B} \cdot \mathbf{A}
\]
- \( \mathbf{B} \): Magnetic field
- \( \mathbf{A} \): Area vector perpendicular to the field
Summary
A magnetic field is a fundamental concept in electromagnetism, representing the influence exerted by magnetic forces. It can be visualized using magnetic field lines and is characterized by properties such as direction,