The Motion in a Straight Line or Rectilinear Motion refers to the motion of an object along a straight line. In this type of motion, the position of the object changes linearly with time along a specific path.

Examples:
-
- A car moving along a straight road.
- A stone dropped from a certain height (neglecting air resistance).
- A child running on a straight track.
Table of Contents
Position (x)
The position of an object is its location in space relative to a chosen reference point or origin. It is a vector quantity, meaning it has both magnitude and direction.
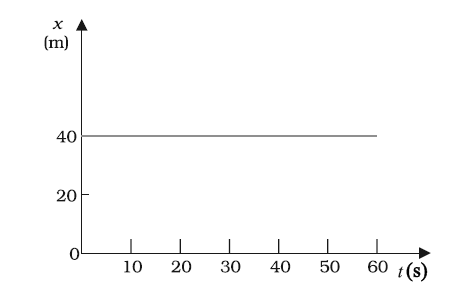
Position Time Graph of Stationary Object
Here the displacement does not change with the change in time.
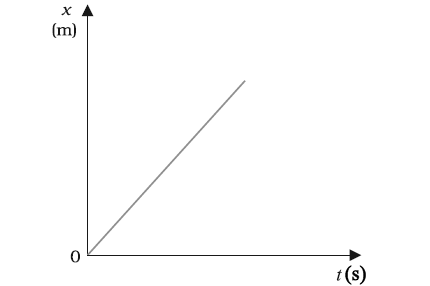
Position Time Graph of an Object in Uniform Motion
The change in displacement is uniform, equal displacement in equal span of time.
Displacement (\(\Delta x\))
The change in position of the object.
\(\Delta x = x_f – x_i\)
- \(x_f\): Final position
- \(x_i\): Initial position
Distance
Distance is the total length of the path traveled by an object, regardless of its direction. Unlike displacement, distance is a scalar quantity and only has magnitude.
Velocity (v)
The rate of change of displacement with time.
Average velocity: \( \bar{v} = \frac{\Delta x}{\Delta t} \)
- \(\Delta t\): Time interval
Instantaneous velocity: The velocity at a specific instant of time, \( v = \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} = \frac{dx}{dt} \)
Acceleration (a)
The rate of change of velocity with time.
Average acceleration: \( \bar{a} = \frac{\Delta v}{\Delta t} \)
- \(\Delta v\): Change in velocity
Instantaneous acceleration: The acceleration at a specific instant of time, \( a = \lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} = \frac{dv}{dt} \)
Equations of Motion for Uniform Acceleration
For rectilinear motion with uniform (constant) acceleration, the following kinematic equations are used:
First Equation: \( v = u + at \)
- \(u\): Initial velocity
- \(v\): Final velocity
- \(a\): Acceleration
- \(t\): Time
Derivation: Acceleration \((a) = (v-u)/ (t)\)
or, \(v-u = at\)
or, \(v = u + at \)
Second Equation: \( s = ut + \frac{1}{2}at^2 \)
- \( u \): Initial velocity
- \( v \): Final velocity
- \( a \): Constant acceleration
- \( t \): Time
- \( s \): Displacement
1. Definition of Velocity
Velocity (\( v \)) is defined as the rate of change of displacement (\( s \)) with respect to time (\( t \)).
\[
v = \frac{ds}{dt}
\]
2. Using the First Equation of Motion
From the first equation of motion, we know that:
\[
v = u + at
\]
3. Substituting the First Equation of Motion into the Velocity Definition
Substitute \( v = u + at \) into \( v = \frac{ds}{dt} \):
\[
\frac{ds}{dt} = u + at
\]
4. Separating Variables
We can separate the variables to integrate both sides with respect to their respective variables.
\[
ds = (u + at) \, dt
\]
5. Integrating Both Sides
Integrate both sides with respect to their respective variables. For the left side, integrate with respect to \( s \), and for the right side, integrate with respect to \( t \).
\[
\int ds = \int (u + at) \, dt
\]
6. Evaluating the Integrals
- The left side integrates to \( s \) (displacement).
- The right side integrates to \( ut + \frac{1}{2}at^2 \).
\[
s = ut + \frac{1}{2}at^2
\]
7. Final Equation
Thus, the second equation of motion relating displacement, initial velocity, acceleration, and time is:
\[
s = ut + \frac{1}{2}at^2
\]
3. \( v^2 = u^2 + 2as \)
4. \( s = \frac{u+v}{2} \cdot t \)
Third Equation: \( v^2 = u^2 + 2as \)
Variables
- \( u \): Initial velocity
- \( v \): Final velocity
- \( a \): Constant acceleration
- \( s \): Displacement
1. Using the First Equation of Motion
From the first equation of motion, we know that:
\[
v = u + at
\]
2. Expressing Time (\( t \))
We can solve the above equation for time \( t \):
\[
t = \frac{v – u}{a}
\]
3. Using the Definition of Average Velocity
Average velocity (\( \bar{v} \)) can be expressed as:
\[
\bar{v} = \frac{u + v}{2}
\]
4. Using the Definition of Displacement
Displacement (\( s \)) is given by the product of average velocity and time:
\[
s = \bar{v} \cdot t
\]
Substitute the expressions for \( \bar{v} \) and \( t \):
\[
s = \left( \frac{u + v}{2} \right) \left( \frac{v – u}{a} \right)
\]
5. Simplifying the Expression
Simplify the right-hand side of the equation:
\[
s = \frac{(u + v)(v – u)}{2a}
\]
6. Expanding the Numerator
Expand the numerator using the difference of squares:
\[
s = \frac{v^2 – u^2}{2a}
\]
7. Solving for \( v^2 \)
Multiply both sides by \( 2a \) to isolate \( v^2 \) on one side of the equation:
\[
2as = v^2 – u^2
\]
Rearrange to solve for \( v^2 \):
\[
v^2 = u^2 + 2as
\]
Free Fall
Free fall refers to the motion of an object where gravity is the only force acting upon it. This means that air resistance is negligible, and the object accelerates downward due to gravity.
The acceleration due to gravity (\( g \)) is a constant near the Earth’s surface and has a value of approximately \( 9.8 \, \text{m/s}^2 \). This acceleration acts downward toward the center of the Earth.
Equations of Motion for Free Fall
The motion of an object in free fall can be described by the equations of motion, with the acceleration \( a \) replaced by \( g \).
\[
v = u + gt
\]
\[
s = ut + \frac{1}{2}gt^2
\]
\[
v^2 = u^2 + 2gs
\]
- \( u \): Initial velocity (usually 0 if the object is dropped)
- \( v \): Final velocity
- \( g \): Acceleration due to gravity (\( 9.8 \, \text{m/s}^2 \))
- \( t \): Time
- \( s \): Displacement
Initial Conditions
- If an object is dropped from rest, its initial velocity (\( u \)) is 0.
- If an object is thrown upwards or downwards, the initial velocity (\( u \)) is the velocity at which it is thrown.
Upward and Downward Motion
- When an object is thrown upwards, it will decelerate at a rate of \( g \) until it reaches its maximum height, where its velocity becomes 0.
- After reaching the maximum height, it will start to fall back down, accelerating at a rate of \( g \).
Time to Reach Maximum Height
The time to reach the maximum height (\( t_{\text{up}} \)) can be found using:
\[
t_{\text{up}} = \frac{u}{g}
\]
Maximum Height
The maximum height (\( h \)) reached by the object can be calculated using:
\[
h = \frac{u^2}{2g}
\]
Total Time of Flight
The total time of flight (\( T \)) for an object thrown upwards and then falling back to the same height can be found using:
\[
T = \frac{2u}{g}
\]
Questions
Question 3. 1. In which of the following examples of motion, can the body be considered approximately a point object.
(a) A railway carriage moving without jerks between two stations.
Explanation: A railway carriage is relatively large compared to the distance between two stations. However, for the purposes of analyzing its motion over long distances, its size can be neglected, and it can be treated as a point object.
Conclusion: The railway carriage can be considered approximately a point object.
(b) A monkey sitting on top of a man cycling smoothly on a circular track.
Explanation: The combined system of the man and the monkey can be treated as a single object. If the size of this system is small compared to the radius of the circular track, it can be considered a point object.
Conclusion: The monkey and the man can be considered approximately a point object.
(c) A spinning cricket ball that turns sharply on hitting the ground.
Explanation: A spinning cricket ball has a significant size compared to the distance it travels after turning sharply. Its rotational motion and the effect of spin cannot be neglected.
Conclusion: The spinning cricket ball cannot be considered a point object.
(d) A tumbling beaker that has slipped off the edge of a table.
Explanation: A tumbling beaker exhibits complex motion, including rotation and translation. Its size and shape are significant in determining its motion.
Conclusion: The tumbling beaker cannot be considered a point object.
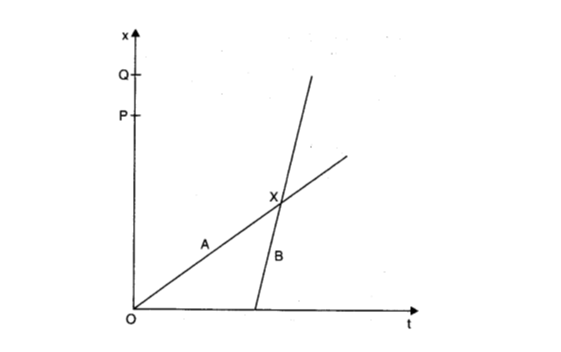
Question 3. 2. The position-time (x -t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in Fig. Choose the correct entries in the brackets below:
(a) (A/B) lives closer to the school than (B/A).
(b) (A/B) starts from the school earlier than (B/A).
(c) (A/B) walks faster than (B/A).
(d) A and B reach home at the (same/different) time.
(e) (A/B) overtakes (B/A) on the road (once/twice).
Solution:
(a) A lives closer to the school as the distance covered by A is OP which is lesser than the distance travelled by B which is OQ.
(b) A starts at the origin whereas B starts after a definite time gap.
(c) As the slope of B is steeper than that of A, B walks faster.
(d) A and B reached the home at the same time.
(e) B overtakes A only once, at the X position in the graph.
Question 3. 3. A woman starts from her home at 9.00 am, walks with a speed of 5 Km/h on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 2.5 km/h. Choose suitable scales and plot the x-t graph of her motion.
Solution:
Step 1: Calculate Times
- Walking time: Distance = 2.5 km, Speed = 5 km/h, Time = Distance/Speed = 0.5 hours = 30 minutes.
- Total time at office: 9:30 AM to 5:00 PM
- Return journey time: Distance = 2.5 km, Speed = 25 km/h, Time = Distance/Speed = 0.1 hour = 6 Minutes
Step 2: Plot the Graph
- From 9:00 AM to 9:30 AM: The woman walks from home (0 km) to office (2.5 km) at a constant speed. This is represented by a straight line with a positive slope.
- From 9:30 AM to 5:00 PM: The woman stays at the office (2.5 km). This is represented by a horizontal line at y = 2.5 km.
- From 5:00 PM to 5:06 PM: The woman returns home (0 km) at a constant speed. This is represented by a straight line with a negative slope.
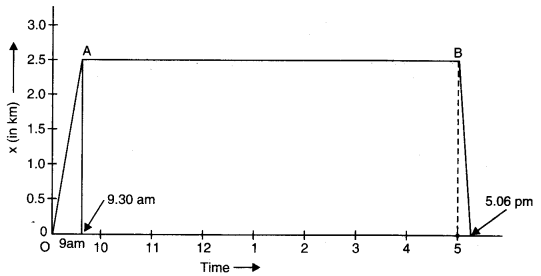
Question 3.4. A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
Solution:
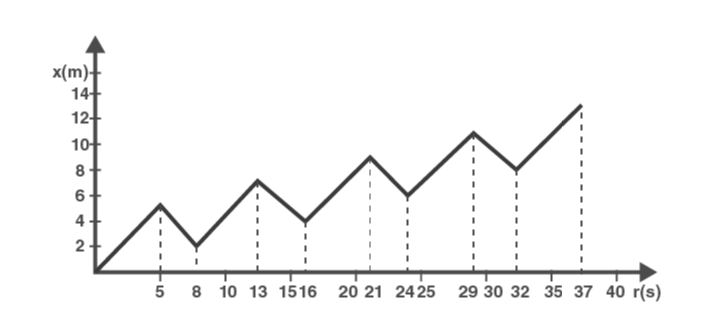
- First Cycle (0 to 8 seconds):
- 5 seconds forward: 5 meters
- 3 seconds backward: \(5 – 3 = 2\) meters
- Second Cycle (9 to 16 seconds):
- 5 seconds forward: \(2 + 5 = 7\) meters
- 3 seconds backward: \(7 – 3 = 4\) meters
- Third Cycle (17 to 24 seconds):
- 5 seconds forward: \(4 + 5 = 9\) meters
- 3 seconds backward: \(9 – 3 = 6\) meters
- Fourth Cycle (25 to 32 seconds):
- 5 seconds forward: \(6 + 5 = 11\) meters
- 3 seconds backward: \(11 – 3 = 8\) meters
- Fifth Cycle (33 to 40 seconds):
- 5 seconds forward: \(8 + 5 = 13\) meters
Thus, after 32 seconds, the drunken will be 8 meters away from the pit. As he takes five more steps forward, he will fall down. So, in total it will take 32 seconds and 5 seconds. In the next second (37th second), he takes one more step forward and reaches 13 meters, falling into the pit.
Question 3.5. A jet airplane travelling at the speed of 500 km/h ejects its products of combustion at the speed of 1500 km/h relative to the jet plane. What is the speed of the latter with respect to an observer on the ground?
Solution: We have a jet plane moving at 500 km/h. The combustion products are ejected at 1500 km/h relative to the jet. We need to find the speed of the combustion products relative to the ground.

Since the combustion products are ejected in the opposite direction of the jet’s motion, we subtract their relative speed from the jet’s speed.
- Speed of combustion products relative to the ground = Speed of jet – Speed of combustion products relative to jet
- Speed of combustion products relative to the ground = 500 km/h – 1500 km/h = -1000 km/h
The negative sign indicates that the combustion products are moving in the opposite direction to the jet, which is backward. Therefore, the speed of the combustion products with respect to an observer on the ground is 1000 km/h backward.
Question 3. 6. A car moving along a straight highway with speed of 126 km h-1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
Solution: We’re asked to find the deceleration (retardation) of a car and the time it takes to stop, given its initial speed and stopping distance.
Step 1: Convert speed to m/s
Initial speed = 126 km/h = (126 * 1000 m) / (3600 s) = 35 m/s
Step 2: Find retardation
We can use the equation of motion:
- v² = u² + 2as Where:
- v = final velocity (0 m/s, as the car stops)
- u = initial velocity (35 m/s)
- a = acceleration (retardation, which is negative)
- s = distance (200 m)
Substituting the values:
- 0² = 35² + 2 * a * 200
- -1225 = 400a
- a = -1225 / 400 = -3.0625 m/s²
So, the retardation of the car is 3.0625 m/s².
Step 3: Find stopping time
We can use the equation:
- v = u + at Where:
- v = final velocity (0 m/s)
- u = initial velocity (35 m/s)
- a = acceleration (retardation, -3.0625 m/s²)
- t = time
Substituting the values:
- 0 = 35 + (-3.0625) * t
- 3.0625t = 35
- t = 35 / 3.0625 = 11.43 seconds
So, it takes 11.43 seconds for the car to stop.
Therefore, the retardation of the car is 3.0625 m/s², and it takes 11.43 seconds for the car to stop.
Question 3. 7. Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 71 km h-1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 ms-1. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
Solution:
Initial speed of both trains = 71 km/h = (71 * 1000 m) / (3600 s) = 20 m/s
- Since both trains are moving in the same direction with the same speed, their initial relative velocity is 0 m/s.
- Relative acceleration (a): This is the acceleration of train B with respect to train A, which is 1 m/s².
- Time (t): 50 seconds
Let d be the distance between the guard of Train A and the Driver of Train B.
So total distance travelled by the driver of Train B will be d + 400 m + 400 m = d+800 m
Using the equation of motion:
- d + 800 = ut + (1/2)at²
- d + 800 = 0 * 50 + (1/2) * 1 * 50²
- d = 450 m
Hence, initial distance between the guard of train A and the driver of train B will be 450 + 400 + 400 = 1250 Meter.
Question 3.8. On a two-lane road, car A is travelling with a speed of 36 km/h. Two cars B and C approach car A in opposite directions with a speed of 54 km/h each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident?
Solution: We have three cars, A, B, and C on a two-lane road. Car A is moving in one direction, while B and C are moving in the opposite direction. Initially, cars A and B are 1 km apart, as are cars A and C. Car B needs to overtake car A before car C does. We need to find the minimum acceleration for car B to achieve this.
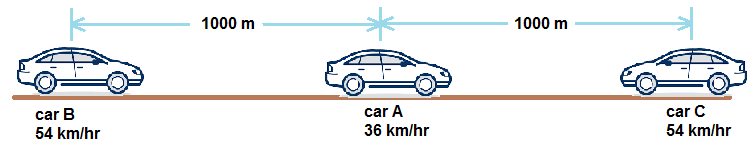
Step 1: Convert speeds to m/s
- Speed of car A = 36 km/h = 10 m/s
- Speed of cars B and C = 54 km/h = 15 m/s
Step 2: Determine the time for car C to overtake car A
The relative speed of car C with respect to car A is 15 m/s + 10 m/s = 25 m/s (as they are moving in opposite directions).
Time taken by car C to overtake car A = Distance / Relative speed = 1000 m / 25 m/s = 40 seconds
Step 3: Calculate the distance car B needs to cover
In the 40 seconds, car A will travel a distance of 10 m/s * 40 s = 400 m.
So, car B needs to cover a total distance of 1000 m (initial distance) + 400 m (distance covered by car A) = 1400 m in 40 seconds to overtake car A before car C.
Step 4: Calculate the required acceleration
Using the equation of motion:
- s = ut + (1/2)at² Where:
- s = distance (1400 m)
- u = initial velocity of car B (15 m/s)
- t = time (40 s)
- a = acceleration
Substituting the values:
- 1400 = 15 * 40 + (1/2) * a * 40²
- 1400 = 600 + 800a
- 800 = 800a
- a = 1 m/s²
Therefore, the minimum acceleration required for car B to overtake car A before car C is 1 m/s².
Question 3. 9. Two towns A and B are connected by regular bus service with a bus leaving in either direction every T minute. A man cycling with a speed of 20 km h-1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road?
Solution: We have two towns, A and B, connected by a bus service with a bus leaving every T minutes in either direction. A cyclist is moving from A to B at 20 km/h. He encounters buses going in the same direction every 18 minutes and buses going in the opposite direction every 6 minutes. We need to find the value of T (bus service period) and the speed of the buses.
- Relative speed of the cyclist and a bus moving in the same direction: Let the speed of the bus be ‘S’ km/h. So, the relative speed is (S – 20) km/h.
- Relative speed of the cyclist and a bus moving in the opposite direction: The relative speed is (S + 20) km/h.
Converting Time to Distance
- Distance covered by the cyclist in 18 minutes: Distance = Speed * Time = (20 km/h) * (18/60) h = 6 km. This is equal to the distance covered by a bus moving in the same direction relative to the cyclist in T minutes.
- Distance covered by the cyclist in 6 minutes: Distance = Speed * Time = (20 km/h) * (6/60) h = 2 km. This is equal to the distance covered by a bus moving in the opposite direction relative to the cyclist in T minutes.
Hence,
- For buses moving in the same direction: \((S – 20) \times \frac{T}{60} = 6\)
- For buses moving in the opposite direction: \((S + 20) \times \frac{T}{60} = 2\)
Solving the Equations
Dividing the first equation by the second, we get:
\(\frac{(S – 20)}{(S + 20)} = 3\)
Solving for S, we get \(S = 40 \text{ km/h}\) (speed of the bus)
Substituting \(S = 40\) in either equation, we get:
\(T = 9 \text{ minutes}\) (bus service period)
Therefore, the period T of the bus service is 9 minutes and the speed of the buses is 40 km/h.
Question 3.10. A player throws a ball upwards with an initial speed of 29.4 ms-1.
(a) What is the direction of acceleration during the upward motion of the ball?
(b) What are the velocity and acceleration of the ball at the highest point of its motion?
(c) Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward, and downward motion.
(d) To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s-2 and neglect air resistance).
Solution:
(a) The direction of acceleration during the upward motion of the ball is downward, towards the center of the Earth. This acceleration is due to gravity and has a magnitude of \(9.8 \, \text{m/s}^2\).
(b) At the highest point of its motion, the velocity of the ball is \(0 \, \text{m/s}\) because it has stopped momentarily before starting to fall back down. The acceleration, however, remains \(9.8 \, \text{m/s}^2\) downward.
(c) Let’s choose \( x = 0 \, \text{m} \) and \( t = 0 \, \text{s} \) at the highest point of the ball’s motion, with the downward direction as positive:
During the upward motion:
-
- Position \( x \) is positive (since it is below the highest point).
- Velocity \( v \) is negative (since it is moving upwards against the positive direction).
- Acceleration \( a \) is positive (since it is downward, same as the positive direction).
During the downward motion:
-
- Position \( x \) is positive (since it is below the highest point).
- Velocity \( v \) is positive (since it is moving downwards in the positive direction).
- Acceleration \( a \) is positive (since it is downward, same as the positive direction).
(d) To find the height the ball rises to and the total time for the ball to return to the player’s hands, we use the following kinematic equations and given data:
Initial speed \( u = 29.4 \, \text{m/s} \),
Acceleration \( a = -9.8 \, \text{m/s}^2 \) (upward motion, opposite to the direction of gravity),
Final speed at the highest point \( v = 0 \, \text{m/s} \).
To find the height \( h \):
\[
v^2 = u^2 + 2a s
\]
\[
0 = (29.4)^2 + 2(-9.8) s
\]
\[
0 = 864.36 – 19.6 s
\]
\[
19.6 s = 864.36
\]
\[
s = \frac{864.36}{19.6} = 44.1 \, \text{m}
\]
The height \( h \) the ball rises is \( 44.1 \, \text{m} \).
To find the time \( t \) to reach the highest point:
\[
v = u + at
\]
\[
0 = 29.4 – 9.8 t
\]
\[
9.8 t = 29.4
\]
\[
t = \frac{29.4}{9.8} = 3 \, \text{s}
\]
The time to reach the highest point is \( 3 \, \text{s} \).
For the total time for the ball to return to the player’s hands, it takes the same amount of time to come down as it does to go up, so:
Total time \( T = 2t = 2 \times 3 = 6 \, \text{s} \).
Therefore, the ball rises to a height of \( 44.1 \, \text{m} \) and returns to the player’s hands after \( 6 \, \text{s} \).
Question 3.11. Read each statement below carefully and state with reasons and examples, if it is true or false; A particle in one-dimensional motion
(a) with zero speed at an instant may have non-zero acceleration at that instant.
(b) with, zero speed may have non-zero velocity.
(c) with constant speed must have zero acceleration,
(d) with positive value of acceleration must be speeding up.
Solution:
(a) True. A particle with zero speed at an instant may have non-zero acceleration at that instant. For example, consider a ball thrown vertically upwards. At the highest point, its speed is zero, but the acceleration due to gravity is \(9.8 \, \text{m/s}^2\) downward.
(b) False. Speed is the magnitude of velocity. If the speed is zero, the magnitude of velocity is also zero. Therefore, a particle with zero speed cannot have a non-zero velocity.
(c) True. A particle with constant speed must have zero acceleration. Acceleration is the rate of change of velocity. If the speed (magnitude of velocity) is constant, the velocity does not change, implying zero acceleration.
(d) False. A positive value of acceleration does not necessarily mean the particle is speeding up. If the acceleration is positive but the velocity is negative (i.e., the particle is moving in the opposite direction), the particle will be slowing down. For example, a car moving backward (negative velocity) and decelerating (positive acceleration) is slowing down.
Question 3. 12. A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t =0 to 12 s.
Solution: A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Let’s calculate the speed-time graph of its motion between \( t = 0 \) to \( t = 12 \) seconds.
Step 1: Calculate the initial speed when the ball hits the floor for the first time.
Using the equation of motion: \[ v^2 = u^2 + 2gh \]
Since the ball is dropped, \( u = 0 \), \( g = 9.8 \, \text{m/s}^2 \), and \( h = 90 \, \text{m} \).
\[ v = \sqrt{2gh} = \sqrt{2 \times 9.8 \times 90} = \sqrt{1764} = 42 \, \text{m/s} \]
Step 2: After the first collision, the ball loses one tenth of its speed, so the speed becomes \( 0.9 \times 42 = 37.8 \, \text{m/s} \).
Step 3: Calculate the time to fall from 90 m.
Using the equation of motion: \[ h = \frac{1}{2}gt^2 \]
\[ 90 = \frac{1}{2} \times 9.8 \times t^2 \]
\[ t^2 = \frac{90 \times 2}{9.8} = \frac{180}{9.8} = 18.37 \]
\[ t = \sqrt{18.37} \approx 4.29 \, \text{s} \]
Step 4: The time to rise back to the height after collision (considering \( g \) and new speed):
Using the equation of motion: \[ v = u + at \]
\[ 0 = 37.8 – 9.8t \]
\[ t = \frac{37.8}{9.8} \approx 3.86 \, \text{s} \]
Step 5: Plotting the speed-time graph for each bounce considering the speed decreases by 10% each time and the duration for each up and down motion:
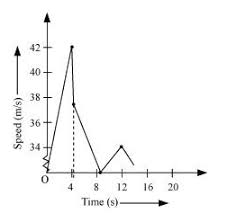
-
- First fall: \( 0 \) to \( 42 \, \text{m/s} \) in \( 4.29 \, \text{s} \)
- First rise: \( 42 \) to \( 0 \, \text{m/s} \) in \( 3.86 \, \text{s} \)
- Second fall: \( 0 \) to \( 37.8 \, \text{m/s} \) in \( 3.86 \, \text{s} \)
- Second rise: \( 37.8 \) to \( 0 \, \text{m/s} \) in \( 3.47 \, \text{s} \)
Question 3.13. Explain clearly, with examples, the distinction between:
(a) Magnitude of displacement (sometimes called distance) over an interval of time, and the total length of path covered by a particle over the same interval;
(b) Magnitude of average velocity over an interval of time, and the average speed over the same interval. (Average speed of a particle over an interval of time is defined as the total path length divided by the time interval). Show in both (a) and (b) that the second quantity is either greater than or equal to the first. When is the equality sign true? [For simplicity, consider one dimensional motion only]
Ans: Distinction between Displacement and Distance, Velocity and Speed
(a) Magnitude of Displacement vs. Total Path Length
- Magnitude of displacement is the shortest distance between the initial and final positions of a particle. It is a vector quantity and has both magnitude and direction. However, we are only concerned with the magnitude here.
- Total path length is the actual distance traveled by the particle, regardless of the direction. It is a scalar quantity and has only magnitude.
Example: Imagine a car moving on a straight road. It travels 5 km east, then turns around and travels 3 km west.
- The magnitude of displacement is 2 km (east).
- The total path length is 8 km (5 km + 3 km).
As you can see, the total path length is always greater than or equal to the magnitude of displacement. The equality sign holds only when the particle moves in a straight line without changing its direction.
(b) Magnitude of Average Velocity vs. Average Speed
- Magnitude of average velocity is the magnitude of the displacement divided by the time interval.
- Average speed is the total path length divided by the time interval.
Example: Using the same example as above, if the car took 2 hours for the entire journey:
- The magnitude of average velocity is 2 km / 2 hours = 1 km/h (east).
- The average speed is 8 km / 2 hours = 4 km/h.
Again, the average speed is always greater than or equal to the magnitude of average velocity. The equality sign holds only when the particle moves in a straight line without changing its direction.
In summary:
- Displacement is concerned with the overall change in position, while distance considers the actual ground covered.
- Velocity is concerned with the rate of change of displacement, while speed is concerned with the rate of change of distance.
Both distance and speed are scalar quantities, while displacement and velocity are vector quantities.
Question 3.14. A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km/h .Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km/h What is the (a)Magnitude of average velocity, and (b)Average speed of the man over the interval of time (i) 0 to 30 min. (ii) 0 to 50 min. (iii) 0 to 40 min? [Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero!]
Ans: We have a man walking to and from the market. We need to calculate the average velocity and average speed for different time intervals.
Given Data
- Distance to market = 2.5 km
- Speed while going to market = 5 km/h
- Speed while coming back home = 7.5 km/h
Time taken to reach the market
- Time = Distance / Speed = 2.5 km / 5 km/h = 0.5 h = 30 minutes
Average velocity = Total displacement / Total time
Average speed = Total distance / Total time
(i) 0 to 30 minutes
-
The man reaches the market.
-
Total displacement = 2.5 km (towards market)
-
Total distance = 2.5 km
-
Total time = 30 minutes = 0.5 h
-
Average velocity = 2.5 km / 0.5 h = 5 km/h (towards market)
-
Average speed = 2.5 km / 0.5 h = 5 km/h
(ii) 0 to 50 minutes
-
The man reaches the market in 30 minutes and then walks back for 20 minutes.
-
Time taken to come back = 20 minutes = 1/3 h
-
Distance covered while coming back = 7.5 km/h × (1/3) h = 2.5 km
-
Total displacement = 2.5 km – 2.5 km = o km
-
Total distance = 2.5 km + 2.5 km = 5 km
-
Total time = 50 minutes = 5/6 h
-
Average velocity = 0 km / (5/6) h = 0 km/h
-
Average speed = 5 km / (5/6) h = 6 km/h
(iii) 0 to 40 minutes
-
The man reaches the market in 30 minutes and then walks back for 10 minutes.
-
Time taken to come back = 10 minutes = 1/6 h
-
Distance covered while coming back = 7.5 km/h × (1/6) h = 1.25 km
-
Total displacement = 2.5 km – 1.25 km = 1.25 km (towards market)
-
Total distance = 2.5 km + 1.25 km = 3.75 km
-
Total time = 40 minutes = 2/3 h
-
Average velocity = 1.25 km / (2/3) h = 1.875 km/h (towards market)
-
Average speed = 3.75 km / (2/3) h = 5.625 km/h
Conclusion: As you can see, in case (ii), the average velocity is zero, while the average speed is non-zero. This clearly shows why average speed is a better representation of the overall motion of the man. Telling him his average speed is zero after walking for 50 minutes would be misleading.
Question 3. 15. In Exercises 3.13 and 3.14, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider instantaneous speed and magnitude of velocity. The instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
Ans: Instantaneous speed is the magnitude of the instantaneous velocity. This is always true because:
Instantaneous velocity is a vector quantity that describes both the speed and direction of an object at a specific point in time. It can be represented by a vector arrow. whereas, instantaneous speed is a scalar quantity that describes only the magnitude (size) of the instantaneous velocity. It is the length of the velocity vector.
When we consider an infinitesimally small time interval (an instant), the path taken by an object is essentially a straight line. This means that the distance traveled and the magnitude of displacement become equal in that instant. As a result, the instantaneous speed (distance/time) and the magnitude of instantaneous velocity (displacement/time) become identical.
Question 3. 16. Look at the graphs (a) to (d) in Fig. 3.20 carefully and state, with reasons, which of these cannot possibly represent one-dimensional motion of a particle.
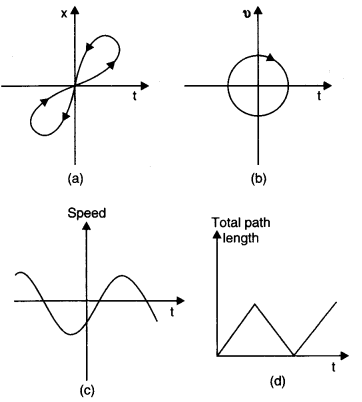
Solution:
(a) It does not represent one-dimensional motion of a particle. A particle cannot have two positions at the same instant of time during its journey.
(b) It does not represent one-dimensional motion of the particle. A particle can never have two values of velocity at the same instant of time.
(c) It does not represent one-dimensional motion of the particle. The speed is a scalar quantity and cannot be negative.
(d) It does not represent one-dimensional motion of the particle. The total path length travelled by the particle cannot decrease with time.
Question 3. 17. Figure shows the x-t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t < 0 and on a parabolic path for t > 0? If not, suggest a suitable physical context for this graph.
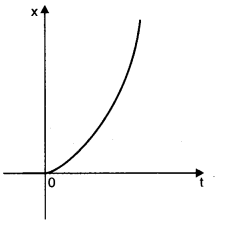
Solution:
For \( t < 0 \):
The displacement \( x \) is zero. This indicates that the particle is at rest at the origin before \( t = 0 \).
For \( t > 0 \):
The x-t graph is parabolic. A parabolic x-t graph suggests that the position \( x \) of the particle changes with the square of time \( t \). This implies that the motion of the particle can be described by a quadratic equation \( x(t) = kt^2 \) (where \( k \) is a constant).
Conclusion: It is not correct to say that the particle moves in a straight line for \( t < 0 \) because the particle is actually at rest (no motion, \( x = 0 \)) during this interval. For \( t > 0 \), the particle does not move on a parabolic path in space, but rather, its position changes parabolically with time, indicating uniformly accelerated motion along a straight line.
- For \( t < 0 \): The particle is stationary at the origin.
- For \( t > 0 \): The particle undergoes uniformly accelerated motion along a straight line.
Question 3. 18. A police van moving on a highway with a speed of 30 km/h fires a bullet at a thief s car speeding away in the same direction with a speed of 192 km/h . If the muzzle speed of the bullet is 150 m/s , with what speed does the bullet hit the thief s car? (Note: Obtain that speed which is relevant for damaging the thief s car).
Solution:
- Speed of police van: \( v_p = 30 \, \text{km/h} \)
- Speed of thief’s car: \( v_t = 192 \, \text{km/h} \)
- Muzzle speed of the bullet: \( v_b = 150 \, \text{m/s} \)
Conversion of Speeds:
\( v_p = 30 \, \text{km/h} = \frac{30 \times 1000}{3600} \, \text{m/s} = 8.33 \, \text{m/s} \)
\( v_t = 192 \, \text{km/h} = \frac{192 \times 1000}{3600} \, \text{m/s} = 53.33 \, \text{m/s} \)
Speed of the Bullet Relative to the Police Van:
The bullet is fired from the police van, so its speed relative to the ground is the sum of the muzzle speed and the speed of the van:
\( v_b’ = v_b + v_p = 150 \, \text{m/s} + 8.33 \, \text{m/s} = 158.33 \, \text{m/s} \)
Relative Speed of the Bullet with Respect to the Thief’s Car:
To find the speed at which the bullet hits the thief’s car, we need to determine the relative speed between the bullet and the thief’s car:
\( v_{\text{rel}} = v_b’ – v_t = 158.33 \, \text{m/s} – 53.33 \, \text{m/s} = 105 \, \text{m/s} \)
The bullet hits the thief’s car with a relative speed of \( 105 \, \text{m/s} \).
Question 3.19. Suggest a suitable physical situation for each of the following graphs:
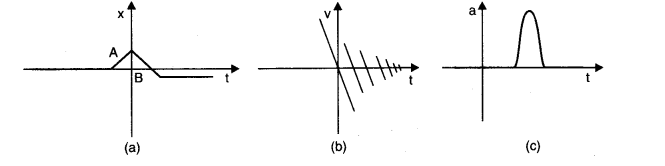
Solution:
(a) It represents a situation where a ball is kicked against a wall horizontally. The ball strikes the wall and returns to the back wall behind the observer striking the ball and stops near the wall.
(b) A user throws the ball upwards with some speed, the speed becomes zero when the ball reaches at the top most points of the journey. Ball hits back on the ground and loses some speed again the same cycle repeats.
(c) The acceleration is zero initially, it means that the particle is moving with a constant velocity. Acceleration increase gradually and attains a peak and decreases gradually to become zero. It is like a rocket going from Earth surface to space with a constant velocity. The extra fuel is pumped and the acceleration increases gradually and comes down to zero when the extra fuel is over.
Question 3. 20. Figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. (You will learn about this motion in more detail in Chapter 14). Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
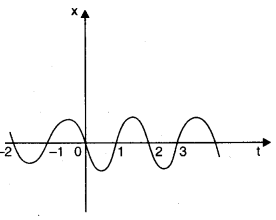
Ans: In Simple Harmonic Motion, acceleration, a = – kx.
(i) At t = 0.3 s, x < 0 i.e., Displacement is negative. dx/xt is negative. as x is becoming more negative with time, it shows that v is also – ve (i.e., v < 0). However, a = -kx will be +ve (a > 0).
(ii) At t = 1.2 s, x > 0, v > 0 and a < 0.
(iii) At t = -1.2 s, x < 0, but here on increasing the time t, value of x becomes less negative. It means that v is +ve (i.e., v > 0). Again a = – kx will be positive (i.e., a > 0).
Question 3.21. Figure gives the x-t plot of a particle in one-dimensional motion. Three different equal intervals of time are shown. In which interval is the average speed greatest, and in which is it the least? Give the sign of average velocity for each interval.
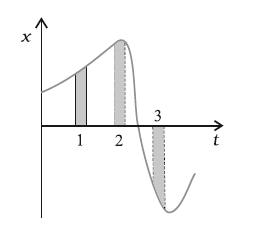
Solution: The average speed is greatest in the interval 3 as the slope of the x-t graph is most steep. Average speed is least in the interval 2 as slope is close to zero. Average velocity will be positive in the intervals 1 and 2. Average velocity is negative in the third interval.
Question 3.22. Figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at points A, B, C and D?
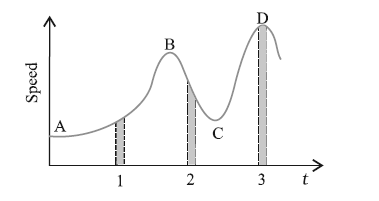
Solution:
- Average acceleration is greatest in magnitude in interval 2 as the slope of speed-time curve is most steep in this interval.
- Average speed is greatest in interval 3 as the magnitude of the speed is maximum in this interval.
- v is positive in all three intervals.
- a is positive in intervals 1, negative in interval 2 as the slope is negative in this interval. a is zero in the interval 3.
- Acceleration at points A, B, C, and D is zero due to zero slope.
Question 3.23. A three – wheeler starts from rest , accelerates uniformly with 1 m/s2 on a straight road for 10 s, and then moves with uniform velocity .plot the distance covered by the vehicle during the n th second (n=1,2,3……..) versus n. what do you expect this plot to be during accelerated motion: a straight line or a parabola?
Solution:
Given Data:
- Initial velocity (\(u\)) = 0 m/s (since it starts from rest)
- Acceleration (\(a\)) = 1 m/s²
- Time of acceleration (\(t\)) = 10 s
Distance Covered During the nth Second
The distance covered during the nth second is given by the difference between the total distance covered in \(n\) seconds and the total distance covered in \((n-1)\) seconds.
The distance covered in \(n\) seconds for uniformly accelerated motion is given by:
\[
s_n = u n + \frac{1}{2} a n^2
\]
Since the initial velocity (\(u\)) is 0, this simplifies to:
\[
s_n = \frac{1}{2} a n^2
\]
The distance covered in \((n-1)\) seconds is:
\[
s_{n-1} = \frac{1}{2} a (n-1)^2
\]
The distance covered during the nth second (\(d_n\)) is:
\[
d_n = s_n – s_{n-1} = \frac{1}{2} a n^2 – \frac{1}{2} a (n-1)^2
\]
Expanding and simplifying:
\[
d_n = \frac{1}{2} a (n^2 – (n^2 – 2n + 1)) = \frac{1}{2} a (2n – 1) = a \left(n – \frac{1}{2}\right)
\]
Given \(a = 1 \, \text{m/s}^2\), we get:
\[
d_n = n – \frac{1}{2}
\]
Nature of the Plot
Since the equation \(d_n = n – \frac{1}{2}\) is linear in \(n\), the plot of the distance covered during the nth second versus \(n\) will be a straight line.
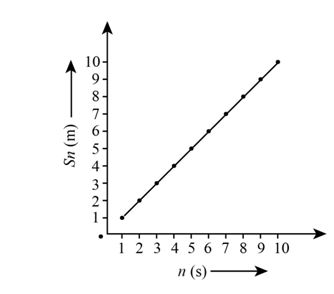
Question 3.24. A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m s-1. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m s-1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
Solution:
Scenario 1: Lift is Stationary
Given Data
- Initial velocity of the ball (\( u \)) = 49 m/s
- Acceleration due to gravity (\( g \)) = 9.8 m/s² (acting downwards)
Time to Reach the Maximum Height
At the maximum height, the final velocity of the ball (\( v \)) is 0 m/s.
Using the kinematic equation:
\[
v = u – g t_1
\]
\[
0 = 49 – 9.8 t_1
\]
Solving for \( t_1 \):
\[
t_1 = \frac{49}{9.8} = 5 \text{ s}
\]
Total Time to Return to Hands
The ball takes the same amount of time to come down as it takes to go up. Thus, the total time (\( T \)) is:
\[
T = 2 t_1 = 2 \times 5 = 10 \text{ s}
\]
Scenario 2: Lift Moving Up with Uniform Speed
Given Data:
- Speed of the lift (\( v_{\text{lift}} \)) = 5 m/s
- Initial velocity of the ball relative to the lift (\( u \)) = 49 m/s
- Acceleration due to gravity (\( g \)) = 9.8 m/s² (acting downwards)
Time to Reach the Maximum Height:
In this case, the relative motion between the lift and the ball does not affect the time taken for the ball to reach the maximum height or return to the boy’s hands because the initial velocity of the ball relative to the boy (in the lift) is the same.
Thus, the time to reach the maximum height (\( t_1 \)) is still:
\[
t_1 = 5 \text{ s}
\]
Total Time to Return to Hands:
The total time (\( T \)) remains:
\[
T = 2 t_1 = 2 \times 5 = 10 \text{ s}
\]
Conclusion: In both scenarios, whether the lift is stationary or moving up with a uniform speed, the time taken for the ball to return to the boy’s hands is the same: 10 seconds.
Question 3.25. On a long horizontally moving belt (Fig.), a child runs to and fro with a speed 9 km/h (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km/h . For an observe a stationary platform outside, what is the
(a) Speed of the child running in the direction of motion of the belt?
(b) Speed of the child running opposite to the direction of motion of the belt?
(c) Time taken by the child in (a) and (b)?
Which of the answers alter if motion is viewed by one of the parents?
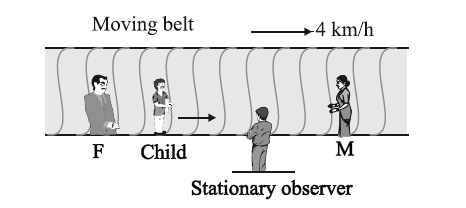
Solution:
Given Data:
- Speed of the child with respect to the belt (\(v_{\text{child, belt}}\)) = 9 km/h
- Speed of the belt (\(v_{\text{belt}}\)) = 4 km/h
- Distance between the father and mother on the belt = 50 m (0.05 km)
(a) Speed of the child running in the direction of motion of the belt:
When the child runs in the direction of the belt’s motion, the speeds add up:
\[
v_{\text{child, direction}} = v_{\text{child, belt}} + v_{\text{belt}} = 9 \text{ km/h} + 4 \text{ km/h} = 13 \text{ km/h}
\]
(b) Speed of the child running opposite to the direction of motion of the belt:
When the child runs opposite to the belt’s motion, the speeds subtract:
\[
v_{\text{child, opposite}} = v_{\text{child, belt}} – v_{\text{belt}} = 9 \text{ km/h} – 4 \text{ km/h} = 5 \text{ km/h}
\]
(c) Time taken by the child in (a) and (b):
To find the time taken, we need to convert the distance to the same unit as the speed (i.e., kilometers).
\[
\text{Distance} = 50 \text{ m} = 0.05 \text{ km}
\]
Time taken when running in the direction of the belt
\[
t_{\text{direction}} = \frac{\text{Distance}}{v_{\text{child, direction}}} = \frac{0.05 \text{ km}}{9 \text{ km/h}} = \frac{0.05}{9} \text{ hours} \approx 0.0055 \text{ hours} \approx 20 \text{ seconds}
\]
Time taken when running opposite to the direction of the belt
\[
t_{\text{direction}} = \frac{\text{Distance}}{v_{\text{child, direction}}} = \frac{0.05 \text{ km}}{9 \text{ km/h}} = \frac{0.05}{9} \text{ hours} \approx 0.0055 \text{ hours} \approx 20 \text{ seconds}
\]
Which of the answers alter if motion is viewed by one of the parents?
If the motion is viewed by one of the parents standing on the belt, they would see the child’s speed as simply 9 km/h. both (a) and (b) will alter but (c) will remain unchanged.
Question 3.26. Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
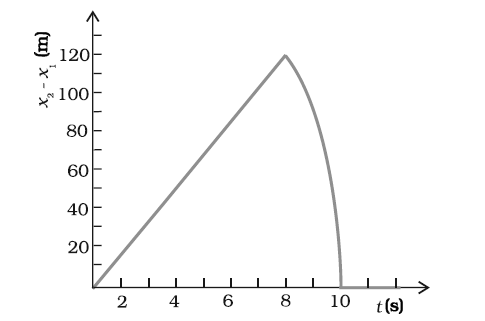
Solution:
Given Data:
- Height of the cliff = 200 m
- Initial speed of stone \( S_1 \) = 15 m/s
- Initial speed of stone \( S_2 \) = 30 m/s
- Acceleration due to gravity \( g \) = 10 m/s²
Equations of Motion
For a stone thrown upwards with an initial velocity \( u \) from a height \( h \), its position \( y \) at time \( t \) is given by:
\[
y = h + ut – \frac{1}{2}gt^2
\]
For Stone \( S_1 \):
\[
y_1 = 200 + 15t – 5t^2
\]
For Stone \( S_2 \):
\[
y_2 = 200 + 30t – 5t^2
\]
Relative Position
The relative position of \( S_2 \) with respect to \( S_1 \) is:
\[
\Delta y = y_2 – y_1 = (200 + 30t – 5t^2) – (200 + 15t – 5t^2)
\]
\[
\Delta y = 30t – 15t = 15t
\]
So, the relative position of \( S_2 \) with respect to \( S_1 \) is a linear function given by:
\[
\Delta y = 15t
\]
Time to Reach the Ground
To find the time at which each stone hits the ground, we set \( y = 0 \).
For Stone \( S_1 \):
\[
0 = 200 + 15t – 5t^2
\]
Solving the quadratic equation:
\[
5t^2 – 15t – 200 = 0
\]
\[
t^2 – 3t – 40 = 0
\]
\[
t = \frac{3 \pm \sqrt{9 + 160}}{2} = \frac{3 \pm 13}{2}
\]
\[
t = 8 \text{ s} \quad (\text{since time cannot be negative})
\]
For Stone \( S_2 \):
\[
0 = 200 + 30t – 5t^2
\]
Solving the quadratic equation:
\[
5t^2 – 30t – 200 = 0
\]
\[
t^2 – 6t – 40 = 0
\]
\[
t = \frac{6 \pm \sqrt{36 + 160}}{2} = \frac{6 \pm 14}{2}
\]
\[
t = 10 \text{ s} \quad (\text{since time cannot be negative})
\]
Hence,
– Stone \( S_1 \) takes 8 seconds to hit the ground.
– Stone \( S_2 \) takes 10 seconds to hit the ground.
Equations for the Linear and Curved Parts of the Plot
Linear Part:
The relative position \( \Delta y = 15t \) is valid until \( t = 8 \) seconds when \( S_1 \) hits the ground.
Curved Part:
After \( S_1 \) hits the ground (at \( t = 8 \) seconds), \( S_1 \) remains at 0 height, and \( S_2 \) continues its motion until it hits the ground (at \( t = 10 \) seconds).
For \( t > 8 \):
– The position of \( S_2 \) can be given by:
\[
y_2 = 200 + 30t – 5t^2
\]
– The relative position after \( t = 8 \) is:
\[
\Delta y = y_2 – 0 = 200 + 30t – 5t^2
\]
So, for \( 8 \leq t \leq 10 \):
\[
\Delta y = 200 + 30t – 5t^2
\]
Summary:
- Relative position (linear part): \( \Delta y = 15t \) for \( t \leq 8 \) s
- Relative position (curved part): \( \Delta y = 200 + 30t – 5t^2 \) for \( 8 \leq t \leq 10 \) s
Question 3. 27. The speed-time graph of a particle moving along a fixed direction is shown in Fig. Obtain the distance traversed by the particle between
(a) t = 0 s to 10 s. (b) t = 2 s to 6 s.
What is the average speed of the particle over the intervals in (a) and (b)?
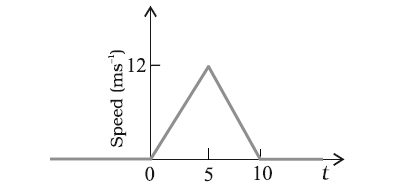
Solution:
(a) From \( t = 0 \) s to \( t = 10 \) s
We need to find the area under the speed-time graph from \( t = 0 \) s to \( t = 10 \) s, which is divided into two triangles:
- First triangle (from \( t = 0 \) s to \( t = 5 \) s):
\[
\text{Area}_1 = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 5 \times 12 = 30 \text{ m}
\]
- Second triangle (from \( t = 5 \) s to \( t = 10 \) s):
\[
\text{Area}_2 = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 5 \times 12 = 30 \text{ m}
\]
Total distance traversed from \( t = 0 \) s to \( t = 10 \) s:
\[
\text{Total distance} = \text{Area}_1 + \text{Area}_2 = 30 + 30 = 60 \text{ m}
\]
(b) From \( t = 2 \) s to \( t = 6 \) s
We need to find the area under the speed-time graph from \( t = 2 \) s to \( t = 6 \) s. This section is divided into two parts:
- Trapezoid (from \( t = 2 \) s to \( t = 5 \) s):
\[
\text{Area}_{\text{trapezoid}} = \frac{1}{2} \times (\text{base}_1 + \text{base}_2) \times \text{height} = \frac{1}{2} \times (4.8 + 12) \times 3 = \frac{1}{2} \times 16.8 \times 3 = 25.2 \text{ m}
\]
- Trapezoid (from \( t = 5 \) s to \( t = 6 \) s):
\[
\text{Area}_{\text{trapezoid}} = \frac{1}{2} \times (\text{base}_1 + \text{base}_2) \times \text{height} = \frac{1}{2} \times (12 + 9.6) \times 1 = \frac{1}{2} \times 21.6 \times 1 = 10.8 \text{ m}
\]
Total distance traversed from \( t = 2 \) s to \( t = 6 \) s:
\[
\text{Total distance} = \text{Area}_{\text{trapezoid1}} + \text{Area}_{\text{trapezoid2}} = 25.2 + 10.8 = 36 \text{ m}
\]
Average Speed
The average speed is the total distance divided by the time interval.
(a) From \( t = 0 \) s to \( t = 10 \) s
\[
\text{Average speed} = \frac{\text{Total distance}}{\text{Time interval}} = \frac{60 \text{ m}}{10 \text{ s}} = 6 \text{ m/s}
\]
(b) From \( t = 2 \) s to \( t = 6 \) s
\[
\text{Average speed} = \frac{\text{Total distance}}{\text{Time interval}} = \frac{36 \text{ m}}{4 \text{ s}} = 9 \text{ m/s}
\]