Norton’s Theorem

Norton’s Theorem is another fundamental principle in electrical engineering that simplifies the analysis of complex linear circuits. It states that any linear electrical network with voltage and current sources and resistances can be replaced by an equivalent circuit consisting of a single current source (\( I_{N} \)) in parallel with a resistance (\( R_{N} \)) connected to a load.

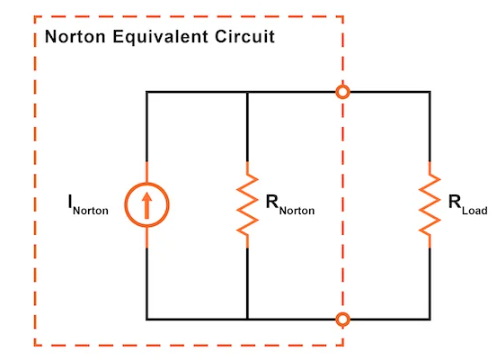
Steps to Apply Norton’s Theorem:

1. Identify the Portion of the Circuit: Select the portion of the circuit to be replaced with the Norton equivalent. Remove the load resistor (\( R_L \)) if present.
2. Calculate \( I_{N} \) (Norton Current):
   • This is the short-circuit current through the terminals where the load resistor was connected.
   • Deactivate all independent sources within the circuit (short circuit all independent voltage sources and open circuit all independent current sources), then calculate the current through a short circuit placed across the open terminals.
3. Calculate \( R_{N} \) (Norton Resistance):
   • This is the equivalent resistance seen from the open terminals after deactivating all independent sources.
   • Short all independent voltage sources and open all independent current sources.
   • Calculate the resistance looking back into the circuit from the open terminals.
4. Reattach the Load Resistor: Reconnect the load resistor to the Norton equivalent circuit.

Example:

Consider a circuit with a voltage source \( V_s \), resistors \( R_1 \), \( R_2 \), and a load resistor \( R_L \).

1. Identify the Portion: Remove \( R_L \) from the circuit.
2. Calculate \( I_{N} \):
   • Determine the short-circuit current through the terminals where \( R_L \) was connected.
   • For instance, if \( R_1 \) and \( R_2 \) are in series and \( R_L \) is connected across \( R_2 \), \( I_{N} \) is the current through \( R_2 \) when a short circuit is placed across the open terminals.
3. Calculate \( R_{N} \):
   • Deactivate the independent sources (short \( V_s \)).
   • Calculate the equivalent resistance seen from the open terminals. If \( R_1 \) and \( R_2 \) are in series, \( R_{N} = R_1 + R_2 \).
4. Reattach the Load Resistor: Reconnect \( R_L \) to the Norton equivalent circuit consisting of \( I_{N} \) in parallel with \( R_{N} \).

Key Points:

• Linear Circuits: Norton’s theorem applies only to linear circuits.
• Simplification: Reduces complex circuits to a simple equivalent circuit, making analysis easier, especially for load variations.
• Versatility: Useful in both AC and DC circuit analysis, with \( I_{N} \) and \( R_{N} \) potentially being complex impedance in AC circuits.

Benefits:

• Simplifies Analysis: Reduces the need for solving complex networks multiple times for different load conditions.
• Intuitive Understanding: Provides an intuitive way to understand the behavior of a circuit at a specific pair of terminals.

Understanding Norton’s theorem is essential for analyzing and designing electrical circuits, as it provides a powerful method for simplifying the analysis of complex networks.