In the field of physics, blackbody radiation is a fundamental concept that explains the electromagnetic radiation emitted by an idealized object known as a blackbody. The spectral distribution of blackbody radiation, also referred to as Planck’s law, plays a crucial role in various scientific disciplines, including astrophysics, quantum mechanics, and thermodynamics.
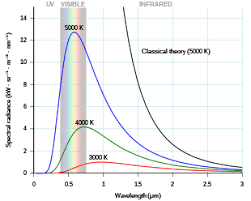
Table of Contents
What is Blackbody Radiation?
A blackbody is an object that absorbs all incident radiation without reflecting or transmitting any of it. It is an idealized concept used to simplify calculations and theoretical models. According to the laws of thermodynamics, a blackbody is in thermal equilibrium, meaning it emits radiation that depends only on its temperature. A blackbody is an idealized object used in physics to simplify calculations and theoretical models.
Key Features of Blackbody Radiation:
- Thermal Equilibrium: A blackbody is assumed to be in thermal equilibrium, meaning its temperature remains constant. This equilibrium state allows the blackbody to emit radiation based solely on its temperature.
- Continuous Spectrum: The radiation emitted by a blackbody covers a wide range of wavelengths or frequencies, resulting in a continuous spectrum. This spectrum extends from ultraviolet (UV) to infrared (IR) wavelengths.
- Intensity Distribution: The spectral distribution of blackbody radiation describes how the intensity of radiation emitted by the blackbody varies with wavelength or frequency. This distribution is characterized by Planck’s law, which accurately describes the behavior of blackbody radiation.
Spectral Distribution of Blackbody Radiation and Planck’s Law
The spectral distribution of blackbody radiation describes how the intensity of radiation emitted by a blackbody varies across different wavelengths or frequencies. Max Planck formulated a mathematical expression known as Planck’s law to describe this distribution accurately.
Planck’s law provides an equation that gives the spectral radiance of blackbody radiation as a function of wavelength (λ) or frequency (ν), temperature (T), and fundamental constants. It can be represented as:
B(λ, T) = (2hc²/λ⁵) * (1/(e^(hc/λkT) – 1))
In the equation:
- B(λ, T) represents the spectral radiance at a particular wavelength λ and temperature T.
- h is Planck’s constant (approximately 6.626 x 10^(-34) J⋅s).
- c is the speed of light (approximately 3 x 10^8 m/s).
- k is the Boltzmann constant (approximately 1.381 x 10^(-23) J/K).
Blackbody Radiation Calculator
Significance of Spectral Distribution
The spectral distribution of blackbody radiation has significant implications across various scientific fields:
a) Astrophysics: The spectral distribution allows astronomers to analyze and interpret the radiation emitted by celestial bodies. It helps determine their temperature, composition, and other important characteristics. The concept of the blackbody spectrum is crucial in understanding the nature of stars, galaxies, and cosmic microwave background radiation.
b) Quantum Mechanics: The quantization of energy levels in atoms and molecules is closely related to blackbody radiation. The spectral distribution assists in studying quantum phenomena, such as emission and absorption spectra, which provide valuable insights into atomic and molecular structures.
c) Thermodynamics: The spectral distribution is fundamental to the study of heat transfer and energy exchange. Understanding blackbody radiation is crucial for designing and optimizing energy systems, such as solar panels, where the conversion of light into usable energy relies on spectral distribution.
Important Links