Star to delta conversion is a technique used in electrical circuits to convert a three-phase system from one configuration to another. This conversion is commonly used in electrical power systems and allows for simplified analysis or when connecting different types of loads or generators. The process involves transforming the connections of resistors, capacitors, or inductors from a star (wye) configuration to a delta (mesh) configuration, or vice versa.
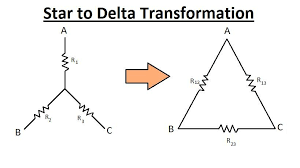
To understand the star-to-delta conversion, let’s consider a three-phase system with three elements (resistors, capacitors, or inductors) labeled A, B, and C, forming a star configuration. The star configuration consists of a common neutral point (N) and three branches (A-N, B-N, and C-N), connecting each element to the neutral point.
Table of Contents
Star-to-Delta Conversion
Delta Configuration (Δ):
R_a =
R_b =
R_c =
The steps for star-to-delta conversion are as follows:
- Identify the three elements labeled A, B, and C in the star configuration.
- Remove the neutral connection (N) and consider the elements A, B, and C as forming a closed-loop triangle, known as a delta (Δ) configuration.
- Assign new labels to the vertices of the delta configuration, typically using lowercase letters, such as a, b, and c, corresponding to the original uppercase labels (A, B, and C).
- Establish relationships between the new and original elements by equating the corresponding values. The relationships depend on whether the elements are resistors, capacitors, or inductors.
- For Resistors: The resistances remain the same. R_a = R_A, R_b = R_B, and R_c = R_C
- For Capacitors: The capacitances change according to the inverse of the original values. C_a = C_A / 3, C_b = C_B / 3, and C_c = C_C / 3
- For Inductors: The inductances change according to the square of the original values. L_a = 3 * L_A, L_b = 3 * L_B, and L_c = 3 * L_C
After performing the star-to-delta conversion, the circuit configuration changes from a star to a delta, allowing for simplified analysis or connection to other delta-connected elements. The reverse process, delta-to-star conversion, follows a similar approach but in reverse, transforming a delta configuration into a star configuration.
It’s important to note that conversion is only applicable when the circuit components have a balanced configuration, meaning the elements in the star configuration have equal magnitudes and phase angles. Otherwise, more complex methods are needed to convert the circuit configuration.
Important Links